電荷が連続的に分布しているときの電位の計算例　面積分

電位の積分による表現において一般的な表式を示した。一般には、電位を求めることは難しいが、 特殊な場合には、求めることが出来る。ここでは、面積分で求める。

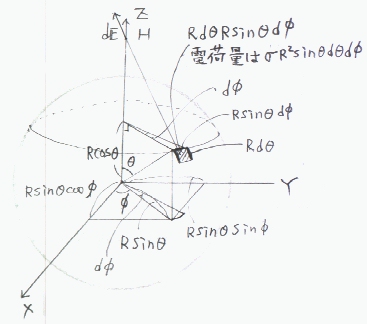
半径Ｒ〔ｍ〕の厚さを無視できる球殻上に均一に面電荷密度 σ〔Ｃ／ｍ^２〕で電荷が分布する場合、球殻の中心からＨ〔ｍ〕での電位を求める　

　球殻の中心にＸＹＺ座標の原点をおき、球殻の中心からＨへの方向にＺ軸をとる。球殻上に点Ｒをとり、その点と原点を結ぶ線のＺ軸からのなす角を θとし、点ＲからＸＹ平面におろした垂線の足と原点を結んだ線（長さはＲsinθ）のＸ軸からのなす角をφとすれば、 θ：０〜π、φ：０〜２π によって球殻上のすべての点を表現できる。θ、φを微小量変化させてえられる球殻上の微小面の面積は、 Ｒd θＲsinθd φで与えられる。 また、この点をＸＹＺ座標であらわせば、 （Ｒsinθcosφ，Ｒsinθsinφ，Ｒcosθ）となる。この微小面上の電荷を点電荷とみなしてＨにおよぼす電位d Φは、 電荷量がσＲd θＲsinθd φ （＝σＲ^２sinθd θd φ）であるので、

d Φ＝	σＲ２sinθd θd φ
	４πε０（（Ｈ−Ｒcosθ）２＋（Ｒsinθ）２））１／２

と表される。

積分範囲を、θ：０〜π、φ：０〜２πとして、積分すれば電位が得られる。

この積分は、φに対しては定数であるので、φについて積分すると２πになる。

Φ＝	∫	d Φ＝	∫	σＲ２sinθd θ
				２ε０（（Ｈ−Ｒcosθ）２＋（Ｒsinθ）２））１／２

cosθ＝μとおけば、d μ＝−sinθd θ（μ：１〜−１）となる。積分範囲を（μ：−１〜１）とすれば、d μ＝sinθd θとおいてよい。

		１
Φ＝	σＲ２	∫	d μ
	２ε０		（Ｈ２＋Ｒ２−２ＨＲμ）１／２
		μ＝−１

ここで、

　

１
∫	d μ
	（Ｈ２＋Ｒ２−２ＨＲμ）１／２
μ＝−１

＝	［	２		］	１
			（Ｈ２＋Ｒ２−２ＨＲμ）１／２
		−２ＨＲ			−１

　　＝−（｜Ｈ−Ｒ｜−｜Ｈ＋Ｒ｜）／ＨＲ

　　＝（｜Ｈ＋Ｒ｜−｜Ｈ−Ｒ｜）／ＨＲ

よって

Φ＝	σＲ２		｜Ｈ＋Ｒ｜−｜Ｈ−Ｒ｜	〔Ｖ〕
	２ε０		ＨＲ

場合分けして表せば、

Ｈ＜Ｒのとき
　Φ＝σＲ／ε_０　〔Ｖ〕

Ｈ＞Ｒのとき
　Φ＝σＲ²／ε_０Ｈ　〔Ｖ〕

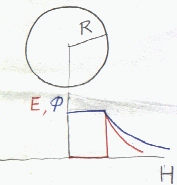
電位（青色）は、電界（赤色）が０の場所では、一定値になる。　

中心からの距離が同じ点は、同電位になる。その点の集合が等電位面になる。(この場合は、球面） （もちろん、もし電界のない空間があれば、等電位'面'ではなく等電位'体'となる（電位の一定値の部分の空間））

電気力線は、正電荷であれば球の表面から外向きに（負電荷なら内に向むきに）まっすぐに放射状にある。

電界は、電位の傾きによって得られる。

Ｈ＝（ｘ，ｙ，ｚ）とすれば、電界Ｅは、

Ｈ＜Ｒのとき

　　　Ｅ＝０　（Φ：一定であるから）

Ｈ＞Ｒのとき

Ｅ＝	σＲ２		（ｘ，ｙ，ｚ）
	ε０（ｘ２＋ｙ２＋ｚ２）		（ｘ２＋ｙ２＋ｚ２）１／２

＝	σＲ２		Ｈ
				〔Ｖ／ｍ〕
	ε０Ｈ２		Ｈ

電界の方向は、正電荷であれば球殻の中心から外に向かう（負電荷なら内に向かう）方向になる。球殻内部では電界は０である。

---

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ