内半径R、肉厚T(外半径R+T)の球殻状に均一に電荷密度 ρ〔C/m3〕で電荷が分布する場合、球殻の中心からHでの電位を求める。

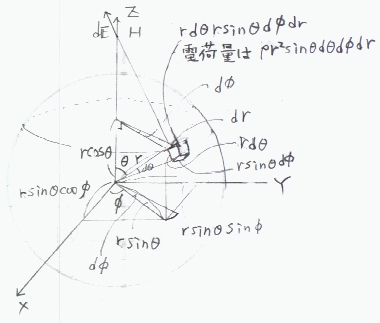
球の中心にXYZ座標の原点をおき、球の中心からHへの方向にZ軸をとる。球内に点rをとり、その点と原点を結ぶ線のZ軸からのなす角を
θとし、点rからXY平面におろした垂線の足と原点を結んだ線(長さはrsinθ)のX軸からのなす角をφとすれば、r:0〜R、θ:0〜π、φ:0〜2π によって球内のすべての点を表現できる。r、θ、φを微小量変化させてえられる球内の微小直方体の体積は、 rrd θrsinθd φ Φは、
電荷量が rrd θrsinθd φ θd φd r)
d Φ= | ρr2sinθd θd φd r |
| 4πε0((H−rcosθ)2+(rsinθ)2)1/2 |
と表される。
(球殻の面積分において球殻の厚みをd rとして半径方向に積み上げる計算を行なう。
半径rの球にd rの厚みを持つ内半径rの球殻をつければ、半径r+d rの球になる。(d rの厚みの半径が0〜Rの球殻を重ね合わせる。)
電位Φは、d Φを積分してあたえられる。積分範囲は、r:R〜R+T、θ:0〜π、φ:0〜2πである。
| R+T | π | 2π | R+T | π | 2π | ||||
| ∫ | ∫ | ∫ | Φ = | ∫ | ∫ | ∫ | ρr2sinθ | φd θd r ・・・(1) | |
| r=R | θ=0 | φ=0 | r=R | θ=0 | φ=0 | ||||
この積分は、φに対しては定数であるので、φについて積分すると2πになる。
| R+T | π | |||
| Φ = | ∫ | ∫ | ρr2sinθ | d θd r ・・・(2) |
| 2ε0(r2−2Hrcosθ+H2)1/2 | ||||
| r=R | θ=0 |
cosθ=μとおけば、d μ=−sinθd μ(μ:1〜−1)となる。積分範囲を(μ:−1〜1)とすれば、 μ=sinθd μ
| R+T | 1 | ||||
| Φ = | ∫ | ρr2 | ∫ | 1 | d μd r ・・・(3) |
| 2ε0 | (r2−2Hrμ+H2)1/2 | ||||
| r=R | μ=−1 |
以前の計算を参考にすれば、
| R+T | ||||
| Φ = | ∫ | ρr2 | |H+r|−|H−r| | d r ・・・(4) |
| 2ε0 | Hr | |||
| r=R |
場合わけしてΦを求める。
H>R+Tのとき
| R+T | |||||
| Φ = | ∫ | ρr2 | d r = | ρ((R+T)3−R3) | 〔V〕 |
| ε0H | 3ε0H | ||||
| r=R |
R<H<R+Tのとき
| H | R+T | |||||||||||||
| Φ = | ∫ | ρr2 | d r + | ∫ | ρr | d r |
= | ρH2 | − | ρR3 | + | ρ(R+T)2 | − | ρH2 |
| ε0H | ε0 | 3ε0 | 3ε0H | 2ε0 | 2ε0 | |||||||||
| r=R | r=H | |||||||||||||
| = | ρ(R+T)2 | − | ρH2 | − | ρR3 | 〔V〕 |
| 2ε0 | 6ε0 | 3ε0 |
H<Rのとき
| R+T | |||||
| Φ = | ∫ | ρr | d r = | ρ((R+T)2−R2) | 〔V〕 |
| ε0 | 2ε0 | ||||
| r=R |
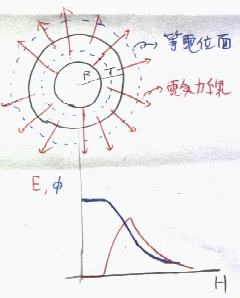
電位(青色)と電界(赤色)を示す。球殻内は、電界0で電位は一定。
中心からの距離が同じ点は、同電位になる。その点の集合が等電位面になる。(この場合は、球面) (もちろん、もし電界のない空間があれば、等電位'面'ではなく等電位'体'となる(電位の一定値の部分の空間))
電気力線は、球殻の内表面から外向きにまっすぐに放射状に伸びる。(球殻の肉厚内部では、表面に近くなるほど電気力線の総数は増加する。)
電界は、電位の傾きによって得られる。
H=(x,y,z)とすれば、電界Eは、上で求めた電位より計算されて、
H<Rのとき
E=0 〔V/m〕 (電位は一定なので)
R<H<R+Tのとき
| E= | ρ | (x,y,z)− | ρR3 | (x,y,z) | |
| 3ε0 | 3ε0(x2+y2+z2) | (x2+y2+z2)1/2 |
| = | ρ | ( | ( | R | ) | 3 | ) | |
| 1− | H 〔V/m〕 | |||||||
| 3ε0 | H |
H>R+Tのとき
| E= | ρ((R+T)3−R3) | (x,y,z) | |
| 3ε0(x2+y2+z2) | (x2+y2+z2)1/2 |
| = | ρ((R+T)3−R3) | H | |
| 〔V/m〕 | |||
| 3ε0H2 | H |
電界の方向は、球殻の中心から外に向かう(負の電荷なら内に向かう)方向になる。