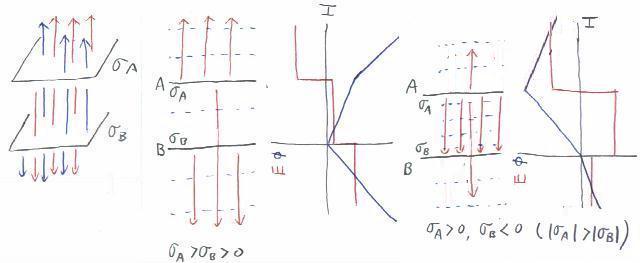
無限の広がりを持つ厚さを無視出来る間隔Tで平行な平面A,B上に均一に面電荷蜜度 σA〔C/m2〕、 σB〔C/m2〕で電荷が分布する場合、平面Bが接地されているとして、BよりHでの電位を求める。
電界は、(例えば)、'96 11/11提出期限のレポートで扱った平行平板と同様に解く。
電界はすべての電荷による電界の合成であることを利用して、電荷をA面とB面に分けてそれぞれの電界を計算し合成すればえられる。
A(B)面の電界は既に求めてあるようにそれぞれの面から垂直に外に向かう方向に、σA/2ε0、 σB/2ε0となる。
それぞれの面による電界を合成すると、電界は3つの領域に分けられ、それぞれの領域内で一様である。
面に垂直にx軸を定めてx軸の原点をB面上に取ってB面からA面に向かう方向を正の方向とし電界をベクトル表示すると、y,z軸がどちらを向いてもBよりxの位置での電界は、
ただし、Ex(x)=(σA+σB)/2ε0 (x>T)、
Ex(x)=(−σA+σB)/2ε, (0<x<T)、
Ex(x)=−(σA+σB)/2ε0 (x<0)
B面の電位を基準として(Φ(0)=0)、Hにおける電位Φ(H)は、電界を積分して
| H | ||
| Φ(H)= − | ∫ | Exd x |
| x=0 |
としてえられる。
H<0のとき、x<0であるから、
| H | |||||||||
| Φ(H)= | ∫ | σA+σB | d x |
= | [ | σA+σB | x | ] | H |
| 2ε0 | 2ε0 | 0 | |||||||
| x=0 |
| = | σA+σB | H | 〔V〕 ・・・(1) |
| 2ε0 |
0<H<Tのとき、0<x<Tであるから、
| H | |||||||||
| Φ(H)= | ∫ | σA−σB | d x |
= | [ | σA−σB | x | ] | H |
| 2ε0 | 2ε0 | 0 | |||||||
| x=0 |
| = | σA−σB | H | 〔V〕 ・・・(2) |
| 2ε0 |
T<Hのとき、0<x<TとT<xでΦ(x)は異なる。式(2)でΦ(T)は得られるので、
| H | |||||||||
| Φ(H)= Φ(T)− | ∫ | σA+σB | d x |
= Φ(T)− | [ | σA+σB | x | ] | H |
| 2ε0 | 2ε0 | T | |||||||
| x=T |
| = | σA−σB | T | − | σA+σB | (H−T) | 〔V〕 ・・・(3) |
| 2ε0 | 2ε0 |
| = | σAT | − | σA+σB | H | 〔V〕 ・・・(3’) |
| ε0 | 2ε0 |

平面からの距離が同じ点は、同電位になる。その点の集合が等電位面になる。(青の破線)
電気力線は、平面から垂直に外向きに(電荷が負なら内向きに)まっすぐに伸びる。(赤の実線)
電界は一定であるので、電気力線は平行で、それぞれの領域で電気力線の密度は変化しない。