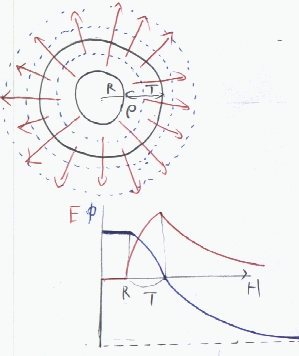
外側表面が接地された内半径R、肉厚T(外半径R+T)の球殻状に均一に電荷蜜度 ρ(C/m3)で電荷が分布する場合、球殻の中心からHでの電位を求める。
電界は、講義のポイントの’電界の計算 2’の項で既に求めた。これを参考にして、中心からxの距離での電界は、
x<Rのとき、 E=0
R<x<R+Tのとき、 E=ρ(x3-R3)/3ε0x2
R+T<xのとき、 E=ρ((R+T)3-R3)/3ε0x2
電界は、球の中心から外に向かう方向
外側表面の電位を基準として(Φ(R+T)=0)Hにおける電位Φ(H)は、球の中心とHを結んだ線(x軸にする)に沿って、電界を積分すれば得られる。
Φ(H)=-∫Ex(x)dx(x;R+T〜H) となる。
R+T<Hのとき
Φ(H)=-∫Ex(x)dx(x;R+T〜H)=-∫ρ((R+T)3-R3)/3ε0x2dx(x;R+T〜H)
=[ρ((R+T)3-R3)/3ε0x](x;R+T〜H)
=ρ((R+T)3-R3)/3ε0*(1/H-1/(R+T))
(Φ(∞)=-ρ((R+T)3-R3)/3ε0*(R+T))
R<H<R+Tのとき
Φ(H)=-∫Ex(x)dx(x;R+T〜H)=-∫ρ(x3-R3)/3ε0x2dx(x;R+T〜H)
=-[ρ/3ε0*(x2/2+R3)/x](x;R+T〜H)
=ρ/3ε0*(((R+T)2-H2)/2+R3)*(1/(R+T)-1/H))
H<Rのとき
Φ(H)=-∫Ex(x)dx(x;R+T〜H)=-∫ρ(x3-R3)/3ε0x2dx(x;R+T〜R)+∫0dx(x;R〜H)
=-[ρ/4ε0*x2-ρR2/2ε0*logx](x;R+T〜R)
=ρ/3ε0*(((R+T)2-R2)/2+R3)*(1/(R+T)-1/R)

球殻の中心からの距離が同じ点は、同電位になる。その点の集合が等電位面になる。(青の破線)
電気力線は、球殻の中心から外に向かう方向で、球殻の内側表面からわき出す外側表面に近づくほど電気力線の総数は増える。(赤の実線)
別解
この電荷分布は、半径R+Tの球状に均一にρで分布した電荷と、半径Rの球状に均一に−ρで分布した電荷の合成と考えることもできる。 電界が、すべての電荷による電界の合成であることを考えれば、半径R+Tで球状に密度ρで分布した電荷の作る電界と、 半径Rで球状に密度−ρで分布した電荷の作る電界との合成になることが分かる。 均一な球状の電荷分布による電界は容易に求まるので、この電界から、球殻の電界を求めて電位を計算することも容易である。