電気双極子の作る電位と電界

十分小さな距離はなれて存在する正負の等量の電荷の組（電荷間の距離に比べて電界（電位）を知りたい点と電荷との距離が十分に大きい）を双極子と言う。 双極子の電界（電位）を求める為に、

点ｒ₁にｑ₁(ｃ)の点電荷、点ｒ₂にｑ₂(ｃ)の点電荷がある時の 点ｒにおける電位と電界の計算法を参考にする。

いま、上の結果を参考にして、電荷より十分離れた位置での電位及び電界の表現を求める。

ｒ₁、ｒ₂が原点近傍にあるとすれば、ｒは原点から十分離れていることになる。

　|ｒ₁|＜＜|ｒ|、|ｒ₂|＜＜|ｒ|

よってｒ_iをΔｒとみたてて一次で近似すれば、

$\Phi ($ｒ)={ｑ₁/4πε₀|ｒ-ｒ₁|}+{ｑ₂/4πε₀|ｒ-ｒ₂|}

　　　={ｑ₁/4πε₀|ｒ|}+grad（ｑ₁/4πε₀|ｒ|）*(-ｒ₁) +{ｑ₂/4πε₀|ｒ|}+grad（ｑ₂/4πε₀|ｒ|）*(-ｒ₂)

もし、ｑ₁=-ｑ₂=ｑならば、

$\Phi ($ｒ)=-grad（{ｑ/4πε₀|ｒ|}）*（ｒ₁-ｒ₂）

ｒ₁-ｒ₂は、点ｒ₂から点ｒ₁へ至るベクトルである。
このベクトルは、|ｒ|に比べて非常に小さいので、δｌとあらわす。1/|ｒ|の傾きは、-ｒ/|ｒ|³であるから

　　　Φ(ｒ)=ｑδｌ*ｒ/4πε₀|ｒ|³

　　　Ｅ=-gradΦ=-ｑδｌ/4πε₀|ｒ|³+3ｑδｌ*ｒｒ/4πε₀|ｒ|⁵

　　　　　　　=-ｑ/4πε₀|ｒ|³*（δｌ-3δｌ*ｒｒ）

　　　　　　　=（ｑ(3δｌ*ｒ)ｒ/|ｒ|²-δｌ）/4πε₀|ｒ|³

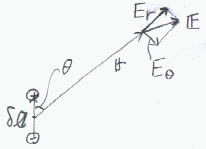
　　δｌの方向を基準にして極座標で表現する。δｌの軸からのｒのなす角をθとすれば、 ｒ=|ｒ|ｅ_r=ｒｅ_r、δｌ=|δｌ|cosθｅ_r-|δｌ|sinθｅ_θであるので、

　　Ｅ=（ｑ(3|δｌ|cosθｅ_r-(|δｌ|cosθｅ_r-|δｌ|sinθｅ_θ)）/4πε₀ｒ³

　　　　　　　=ｑ（2|δｌ|cosθｅ_r+|δｌ|sinθｅ_θ）/4πε₀ｒ³

　　　　　　　=（2|ｑδｌ|cosθｅ_r+|ｑδｌ|sinθｅ_θ）/4πε₀ｒ³

となる。（傾きの演算については、ベクトル（スカラ）の位置変数の微分演算を参照する。

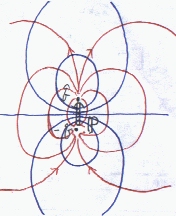
電気力線（赤）（電界は、大きさが電気力線の密度に比例し、電気力線の接線の方向）、等電位面（青）は左のようにかける。

点ｒから見て、電荷がどのような向きに並んでいるかによって電位（電界）は決まる。

小さな距離はなれて存在する正負の等量の電荷の組を双極子と言う。双極子の作る電位（電界）は、正負の電荷量と二極間の距離との積(|ｑδｌ|)と正負の電荷の並ぶ方向(δｌの方向)で決まる。 ベクトルｑδｌで電位（電界）が決まることが分かる。そこで、ｑδｌを電気双極子と呼び、Ｐとあらわす。この結果は、分極で利用する。

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ