閉曲面上の任意の点をrとすれば、点rにおける電界Eは、
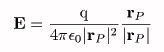
で表される。今、点rで閉曲面S上に微小領域
立体角の考え方を使うので、よく分からない人は勉強する
内積の考え方を使うので、よく分からない人は勉強する
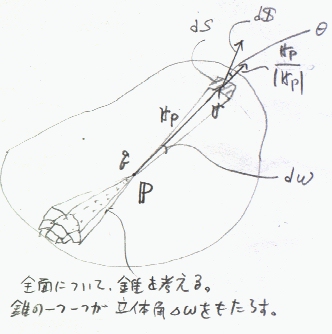
今、右図のようにqなる電荷を点Pにおき、この電荷を包む閉曲面Sを考えるとする。
(閉じた面Sによってqを含む空間(Sの内部)とqを含まない空間(Sの外部)に分離したということ)
閉曲面上の任意の点をrとすれば、点rにおける電界Eは、
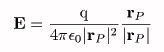
で表される。今、点rで閉曲面S上に微小領域
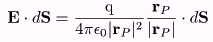
ここで、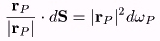
この式は、左辺のベクトルrP/|rP|と
E・d S= |
q | |rP|2d ωP |
|
| 4πε0|rP|2 |
= |
q | d ωP |
|
| 4πε0 |
よって、E・dSは、電荷から微小領域
S上の微小領域dSに対して
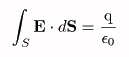
これが、ガウスの定理(積分形式)である。
複数の電荷が閉曲面内にある場合には、それぞれの電荷について、電荷の存在する点を基準に選んでそこから閉曲面を見た立体角を考えれば、
上式が電荷毎に成り立つことが分かる。電荷を含む閉曲面を考えて、閉曲面を(電界が一定と見なせるほどの)微小な面に分割して、そのすべて場所において電界と微小面との内積
ガウスの定理(積分形式)を言葉で表現すれば、
電界を閉曲面上で面との内積を取って面積分した値は、閉曲面内部の電荷量を
もし、電荷が三次元空間で位置rの関数として密度ρ(r)で与えられたとすれば、閉曲面内の空間全体にわたってρ(r)を体積積分すれば、閉曲面内の全電荷qが得られるので、
| q= | ∫ | ρ(r)d V |
| ∫ | 1 | ∫ | |
E・d S = | ρ(r)d V | ||
| ε0 |
'何か'が電荷から出ているとすれば('何か'は、電荷量に比例し、'正なら出る' '負なら吸い込まれる')、適当な(任意の)閉曲面で電荷をくるんで、
閉曲面から出ていく'何か'をすべてたせば、電荷から出た'何か'の量になるので、どのような閉曲面でも(大きくても、小さくても)一定の量(電荷から出た'何か'の総数)になる。もし、適当な閉曲面上で'何か'の量をすべてたせば、閉曲面内の電荷から出た'何か’の総量になる。'何か'は電気力線に相当し、その数は電荷量がQのとき
わら束を垂直に切った場合と斜めに切った場合では、切った断面の面積は異なるが、切断したわらの総本数は同じになる。(内積とはこんなものともいえる。) 電界と(平面にみなせるほどの)微小面積との内積をとるということは、微小面積で切断するわら(電気力線)の本数を得ることに相当する。