電荷が連続的に分布しているときの電界の計算例　線積分

電界の積分による表現において一般的な表式を示した。関数として電界を求めることは、一般には難しいが、 特殊な場合には、求めることが出来る。ここでは、線積分で求める

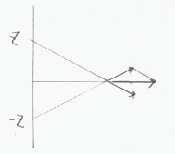
太さを無視できる無限長の線上に均一に線電荷密度λ〔Ｃ／ｍ〕で電荷が分布する場合、線から距離Ｒ〔ｍ〕の場所での電界を求める。

　電荷の分布する線方向にｚ軸をとる。電界を考える点Ｒをｙ軸上に含むようにｙ軸を決めると、 電界はｙｚ面内の成分になり、軸との距離 'Ｒ' によって大きさが来まる。（電界を知りたい点の座標は（Ｒ，０））
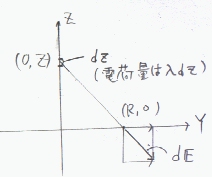
変数 ｚ によって電荷の分布する線は表現されるので、ｚ方向の微小量d ｚで切られる線分を点電荷 （λd ｚ）と見立ててｚについて､−∝〜＋∝まで積分すれば（たせば）、電界が得られる。

ｙｚ座標で点を表現すると、点（０，ｚ）にある微小電荷が点（Ｒ，０）に及ぼす電界d Ｅ（ｚ）は、

d Ｅ（ｚ）＝	λd ｚ		（Ｒ，−ｚ）	・・・（１）
	４πε０（Ｒ２＋ｚ２）		（Ｒ２＋ｚ２）１／２

となる。（１）式を成分に毎に積分すれば、Ｅ_ｙ、Ｅ_ｚは得られる。

	∞
Ｅｙ　＝	∫	Ｒλd ｚ	・・・（２）
		４πε０（Ｒ２＋ｚ２）３／２
	ｚ＝−∞

＝	λ	〔Ｎ／Ｃ〕　　　・・・（２’）
	２πε０Ｒ

	∞
Ｅｚ　＝	∫	−ｚλd ｚ	・・・（３）
		４πε０（Ｒ２＋ｚ２）３／２
	ｚ＝−∞

　　　　　＝　０　　〔Ｎ／Ｃ〕　　　・・・（３’）

　式（２→２’、３→３’）の計算例（積分の計算例）を見る　

　点(0,z)に対して点(0,-z)の電荷による電界を考えると、両者によって電界のZ成分は、打ち消される。 総てのｚ軸上の点において、同様に打ち消されるので、E_ｚ=0となる。（このような考察を行なえば、始めから電界のZ成分は0とおける）

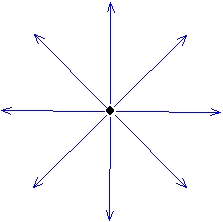
電界は、無限長の線を中心に放射状に外に向かう（電荷が負なら内に向かう）方向で表現される。
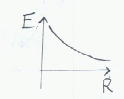
中心からの距離をＲとすれば、電界の強さはグラフのように変化する。（Ｒに対して反比例する）

別解（ガウスの定理を利用）

式（２→２’、３→３’）の計算例（積分の計算例）

（２）、（３）式それぞれにおいて、ｚ＝Ｒtanθと変数変換する。

（θについての積分範囲は　−

π ２

＜θ＜

π ２

）

d ｚ　＝	Ｒd θ	，　　　１＋　tan２θ　＝	１
	cos２θ		cos２θ

であるから、

	π／２
式（２）＝	∫	Ｒλ		Ｒd θ
		４πε０（Ｒ２＋Ｒ２tan２θ）３／２		cos２θ
	θ＝−π／２

積分範囲で、cosθ＞０であるから、

	π／２
＝	∫	λcosθ		d θ
		４πε０Ｒ
	θ＝−π／２

cosθについて積分を行えば、式（２’）になる。

	π／２
式（３）＝	∫	−Ｒtanθλ		Ｒd θ
		４πε０（Ｒ２＋Ｒ２tan２θ）３／２		cos２θ
	θ＝−π／２

積分範囲で、cosθ＞０であるから、

	π／２
＝	∫	−λsinθ		d θ
		４πε０Ｒ
	θ＝−π／２

sinθについて積分を行えば、式（３’）になる。

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ