電荷が連続的に分布しているときの電界の計算例　面積分

電界の積分による表現において一般的な表式を示した。一般には、電界を求めることは、難しいが 特殊な場合には、求めることが出来る。ここでは、面積分で求める。

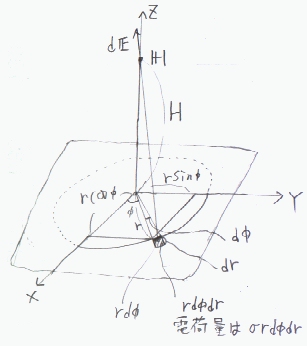
無限の広がりを持つ厚さを無視出来る平面上に均一に面電荷密度（σ〔Ｃ／ｍ^２〕）で電荷が分布する場合、平面の上方Ｈ〔ｍ〕（点Ｈ） での電界を求める。

　Ｈから平面におろした垂線の足をｘｙｚ座標の原点として、Ｈにむかってｚ軸をとる。電荷の分布する平面はｘｙ平面で与えられる。 原点からの距離ｒとｘｙ平面上でのｘ軸からの角度φを変数に選んで、ｘｙ平面上の点をあらわせば、ｒ，φにより点（ｘ，ｙ）は、 ｘ＝ｒcosφ，ｙ＝ｒsinφとかける。変数ｒとφによって作られる微小平面の面積はｒd φd ｒとなる。 この微小平面内の電荷を点電荷とみなしてＨにできる電界d Ｅは、電荷量がσｒd φd ｒであるので、

d Ｅ（φ）＝	σｒd φd ｒ		（−ｒcosφ，−ｒsinφ，Ｈ）	・・・（１）
	４πε０（ｒ２＋Ｈ２）		（ｒ２＋Ｈ２）１／２

と表現される。

Ｅ_ｘ，Ｅ_ｙ，Ｅ_ｚは、ｒ：０〜∞，φ：０〜２πを積分領域として、それぞれの成分を積分すれば得られる。

	∞	２π		∞	２π
Ｅｘ　＝	∫	∫	d Ｅｘ　＝	∫	∫	−σｒ２cosφd φd ｒ	・・・（２）
						４πε０（ｒ２＋Ｈ２）３／２
	ｒ＝０	φ＝０		ｒ＝０	φ＝０

　Ｅ_ｘ＝０　　〔Ｎ／Ｃ〕　　・・・・（２’）

cosφの一周期にわたる積分であるから式（２）の値は’０’になる。
同様にＥ_ｙも計算されて、sinφの一周期にわたる積分であるから’０’になる。

	∞	２π		∞	２π
Ｅｙ　＝	∫	∫	d Ｅｙ　＝	∫	∫	−σｒ２sinφd φd ｒ	・・・（３）
						４πε０（ｒ２＋Ｈ２）３／２
	ｒ＝０	φ＝０		ｒ＝０	φ＝０

　Ｅ_ｙ＝０　　〔Ｎ／Ｃ〕　　・・・・（３’）

Ｅ_ｚは、φに関しては被積分関数が定数であるので、簡単に計算される。

	∞	２π		∞	２π
Ｅｚ　＝	∫	∫	d Ｅｚ　＝	∫	∫	σｒＨd φd ｒ	・・・（４）
						４πε０（ｒ２＋Ｈ２）３／２
	ｒ＝０	φ＝０		ｒ＝０	φ＝０

	∞
＝	∫	σＨｒ	d ｒ　　　・・・（４’）
		２ε０（ｒ２＋Ｈ２）３／２
	ｒ＝０

　式（４’）で、ｒ^２＋Ｈ^２　→　ｔ　の様な変数変換をして積分すれば容易に積分値は求まって、

Ｅｚ＝	σ	Ｈ
			〔Ｎ／Ｃ〕　　・・・（４”）
	２ε０	｜Ｈ｜

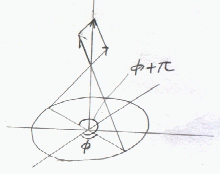
　ｒ，φで与えられる点（ｒcosφ，ｒsinφ）において中心軸に対して反対方向の点（ｒcos（φ＋π），ｒsin（φ＋π））の電荷による電界を考えると、 両者によって電界のｘｙ成分は打ち消される。総ての平面上の点電荷に対して、同様に打ち消されるので、電界のｘ成分,ｙ成分は’０’となる。 （このような考察を行なえば、始めから電界のｘ成分，ｙ成分は’０’としてよいことが分かる。）

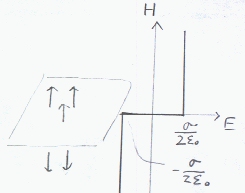
電界は、面に垂直な方向で、面から外に向かう（電荷が負なら内に向かう）方向になる。電界の大きさ（σ／2ε_０〔Ｎ／Ｃ〕）は面からの距離には依存しない。電界を図示する。

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ