電荷が連続的に分布しているときの電界の計算例　体積積分

電界の積分による表現において一般的な表式を示した。一般には、電界を求めることは、難しいが 特殊な場合には、求めることが出来る。ここでは、体積積分で求める。

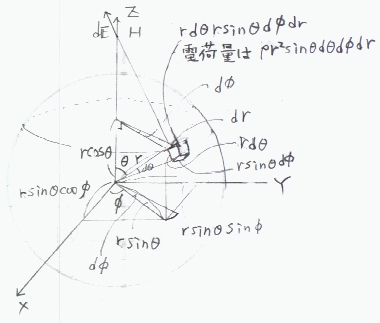
半径Ｒの球内に均一に電荷密度 ρ〔Ｃ／ｍ^３〕で電荷が分布する場合、球の中心からの距離Ｈでの電界を求める。

別解（ガウスの定理を使って求める）

　球の中心にｘｙｚ座標の原点をおき、球の中心からＨへの方向にｚ軸をとる。球内に点ｒをとり、その点と原点を結ぶ線のｚ軸からのなす角を θとし、点ｒからｘｙ平面におろした垂線の足と原点を結んだ線（長さはｒsinθ）のｘ軸からのなす角をφとすれば、ｒ：０〜Ｒ，θ：０〜π， φ：０〜２π によって球内のすべての点を表現できる。ｒ、θ、φを微小量変化させてえられる球内の微小直方体の体積は、d ｒｒd θｒsinθd φで与えられる。また、この点をｘｙｚ座標であらわせば、 （ｒsinθcosφ，ｒsinθsinφ，ｒcosθ）となる。この微小直方体を点電荷とみなしてＨにできる電界d Ｅは、電荷量がρd ｒｒd θｒsinθd φ （＝ρｒ²sinθd θd φd ｒ） であるので、

d Ｅ＝	ρｒ2sinθd θd φd ｒ		（−ｒsinθconφ，−ｒsinθsinφ，Ｈ−ｒcosθ）	・・・（１）
	４πε０（（Ｈ−ｒcosθ）２＋（ｒsinθ）２）		（（Ｈ−ｒcosθ）２＋（ｒsinθ）２）１／２

と表される。

（球殻の面積分において球殻の厚みをd ｒとして半径方向に重ねる計算を行なう。 半径ｒの球にd ｒの厚みを持つ内半径ｒの球殻をつければ、半径ｒ＋d ｒの球になる。（d ｒの厚みを持つ半径が０〜Ｒの球殻を重ね合わせる。）　

Ｅ＝∫d Ｅであるから、電界のそれぞれの座標成分は、

	Ｒ	π	２π		Ｒ	π	２π
Ｅｘ　＝	∫	∫	∫	d Ｅｘ　＝	∫	∫	∫	−ρｒ３sin２θcosφ	d φd θd ｒ　　　・・・（２）
								４πε０（ｒ２−２Ｈｒcosθ＋Ｈ２）３／２
	ｒ＝０	θ＝０	φ＝０		ｒ＝０	θ＝０	φ＝０

	Ｒ	π	２π		Ｒ	π	２π
Ｅｙ　＝	∫	∫	∫	d Ｅｙ　＝	∫	∫	∫	−ρｒ３sin２θsinφ	d φd θd ｒ　　　・・・（３）
								４πε０（ｒ２−２Ｈｒcosθ＋Ｈ２）３／２
	ｒ＝０	θ＝０	φ＝０		ｒ＝０	θ＝０	φ＝０

	Ｒ	π	２π		Ｒ	π	２π
Ｅｚ　＝	∫	∫	∫	d Ｅｚ　＝	∫	∫	∫	−ρｒ２sinθ（Ｈ−ｒcosθ）	d φd θd ｒ　　　・・・（４）
								４πε０（ｒ２−２Ｈｒcosθ＋Ｈ２）３／２
	ｒ＝０	θ＝０	φ＝０		ｒ＝０	θ＝０	φ＝０

Ｅ_ｘ，Ｅ_ｙは、φについて積分すると０になるので、Ｅ_ｘ＝Ｅ_ｙ＝０である。 Ｅ_ｚは、φに対して定数であるので、容易に積分されて、

	Ｒ	π
Ｅｚ　＝	∫	∫	ρｒ２（Ｈ−ｒcosθ）sinθ	d θd ｒ　　　・・・（４’）
			２ε０（ｒ２−２Ｈｒcosθ＋Ｈ２）３／２
	ｒ＝０	θ＝０

θに関する積分は、以前のページを参考（Ｒをｒに読み替える）にして行えば、

　

Ｒ

∫

σｒ２

（

１

（

Ｈ−ｒ

Ｈ＋ｒ

）

｜Ｈ−ｒ｜−｜Ｈ＋ｒ｜

）

Ｅｚ＝

−

−

d ｒ　　　・・・（４”）

２ε０

Ｈｒ

｜Ｈ−ｒ｜

｜Ｈ＋ｒ｜

Ｈ２ｒ

ｒ＝０

　式（４”）において、

Ｈ＜ｒのとき、 　

	σｒ２	（		２		−２Ｈ	）
被積分関数＝			−		−			＝　０　　・・・（５）
	２ε０			Ｈｒ		Ｈ２ｒ

Ｈ＞ｒのとき 　

	σｒ２	（		−２ｒ	）		ρｒ２
被積分関数＝			−			＝		・・・（６）
	２ε０			Ｈ２ｒ			ε０Ｈ２

Ｈ＞Ｒのとき、式（６）を参考にして、

	Ｒ
	∫	ρｒ２
Ｅｚ＝			d ｒ
		ε０Ｈ２
	ｒ＝０

	ρＲ３
＝		〔Ｎ／Ｃ〕　　・・・（７）
	３ε０Ｈ２

Ｈ＜Ｒのとき、積分範囲を二つに分けて、Ｈ＜ｒ＜Ｒで、被積分関数が’０’であることを考慮して、

		Ｈ		Ｒ			Ｈ
	（	∫		∫	）		∫	ρｒ２
Ｅｚ＝			＋			（　（５）または、（６）式　）d ｒ　＝			d ｒ
								ε０Ｈ２
		ｒ＝０		ｒ＝Ｈ			ｒ＝０

	ρＨ
＝		〔Ｎ／Ｃ〕　　・・・（８）
	３ε０

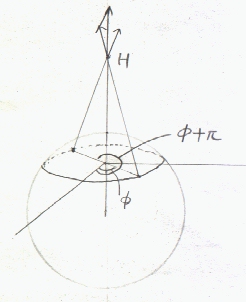
　θ，φで与えられる点（ｒsinθcosφ，ｒsinθsinφ，ｒcosθ）において中心軸に対して反対方向の点 （Ｒsinθcos（φ＋π），Ｒsinθsin（φ＋π），ｒcosθ）の電荷による電界を考えると、 両者によって電界のｘｙ成分は打ち消される。総ての平面上の点において、同様に打ち消されるので、電界のｘ成分，ｙ成分は０となる。 （このような考察を行なえば、積分しなくても電界のｘ成分，ｙ成分は０となることが分かる。）

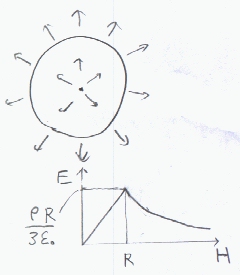
電界は、球の中心から外に向かう（負の電荷なら内に向かう）方向になる。電界を図示する。　

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ