中心からの距離をRとすれば、電界の強さはグラフのように変化する。(Rに対して反比例する)
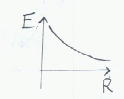
太さを無視できる無限長の線上に均一に線電荷密度λ〔C/m〕で電荷が分布する場合、線から距離Rの場所での電界を求める
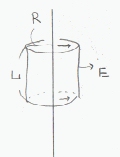
電界は、電荷の分布する無限長の線より垂直に外に向かう方向であるから、電荷の分布する無限長の線を中心軸にした円筒の側面と 電界の方向は垂直である。また、円筒側面上で電界の大きさはすべて等しい。 電荷の分布する線を中心軸にして高さL半径Rの円柱型の閉曲面上でガウスの定理左辺の面積分を行なう。 右辺の電荷総量も求めて両辺が等しいとおき電界を求める。
閉曲面上での電界の大きさをEとすれば、
左辺=∫E・d S(S:円柱側面+円柱上面+円柱下面)
=∫E・d S(S:円柱側面)+∫E・d S(S:円柱上面+円柱下面)
∫E・d S(S:円柱側面)=E∫d S(S:円柱側面)(Eとd Sは同じ方向で、Eは面上で同じ値)
=E2πRL
∫E・d S(S:円柱上面+円柱下面)=0(面上でEとd Sは垂直なので内積は’0’)
左辺=E2πRL
右辺=λL/ε0
左辺=右辺より、2πRLE=λL/ε0
E=λ/2πε0R 〔N/C〕(λ>0(λ<0)なら、線から外(内)に向かう方向)
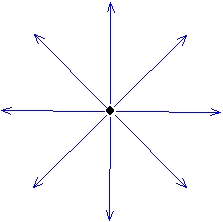
答を図示する
電気力線は、無限長の線を中心に放射状に外に向かう(電荷が負なら内に向かう)方向で表現される。
中心からの距離をRとすれば、電界の強さはグラフのように変化する。(Rに対して反比例する)
