内半径R、肉厚T(外半径R+T)の無限長円筒(無限に長いちくわ)状に電荷密度ρ〔C/m3〕で電荷が分布する場合、 円筒の中心から距離Hの場所での電界を求める
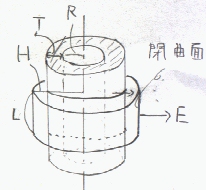
電界は、電荷の分布する無限長のちくわより垂直に外に向かう方向であるから、 電荷の分布する無限長のちくわの中心を中心軸にした円筒の側面と電界の方向は垂直である。また、円筒側面上で電界の大きさはすべて等しい。 電荷の分布するちくわの中心を中心軸にして長さL半径Hの円柱型の閉曲面上でガウスの定理左辺の面積分を行なう。 右辺の電荷総量も求めて両辺を等しいとおき電界を求める。
距離Hにおける円柱側面での電界の大きさをEとすれば、
左辺=∫E・d S(S:円柱側面+円柱上面+円柱下面)
=∫E・d S(S:円柱側面)+∫E・d S(S:円柱上面+円柱下面)
∫E・d S(S:円柱側面)=E∫d S(S:円柱側面)(Eとd Sは同じ方向で、Eは面上で同じ値)=E2πHL
∫E・d S(S:円柱上面+円柱下面)=0(面上でEとd Sは垂直なので内積は’0’)
左辺=E2πHL
右辺=0;(H<R)、ρπ(H2−R2)L/ε0;(R<H<R+T)、 ρπ((R+T)2−R2)L/ε0;(R+T<H)
左辺=右辺より、
H<Rのとき E=0 〔N/C〕
R<H<R+Tのとき E=ρ(H2−R2)/2Hε0 〔N/C〕
R+T<Hのとき E=ρ(2RT+T2)/2Hε0 〔N/C〕
電界は、λ>0(λ<0)なら、無限長円筒の中心軸から外(内)に向かう方向
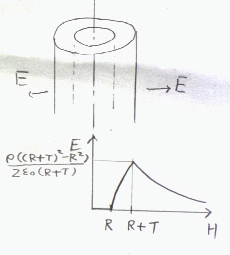
答を図示する
電界は、無限長円筒の中心軸から放射状に外に向かう(電荷が負なら内に向かう)方向になる。中心からの距離をRとすれば、右のように描ける。