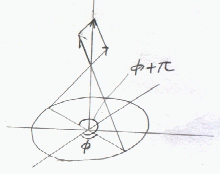
無限の広がりを持つ厚さを無視できる平面上に均一に面電荷密度 σ〔C/m2〕で電荷が分布する場合、平面の上方Hでの電界を求める。
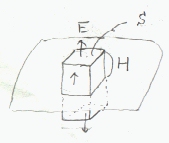
電界は、σ>0では、電荷の分布する無限平面より垂直に外(上下)に向かう方向であるから、電荷の分布する無限平面を中心に上下に高さを持つ柱の側面内に、電界の方向はある。また、柱上面と下面では、電界は外向きに面に垂直で、大きさが等しい。
電荷の分布する面を中心にして上下に高さH、断面積Aの柱型の閉曲面上でガウスの定理左辺の面積分を行なう。 右辺の電荷総量も求めて両辺が等しいとおき電界を求める。
閉曲面上での電界の大きさをEとすれば、
左辺=∫E・d S(S:柱側面+柱上面+柱下面)=∫E・d S(S:柱側面)+∫E・d S(S:柱上面+柱下面)
∫E・d S(S:柱側面)=0(面上でEとd Sは垂直なので内積は’0’)
∫E・d S(S:柱上面+柱下面)=2EA
左辺=2EA
右辺=σA/ε0
左辺=右辺より、2EA=σA/ε0
E=σ/2ε0 〔N/C〕 (σ>0(σ<0)面から外に(面に)向かう方向)
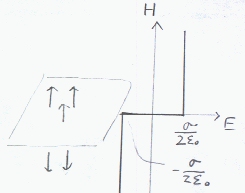
答を図示する
電界は、無限平面を中心に垂直に外に向かう(電荷が負なら内に向かう)方向で表現される。電界は、平面からの距離にはよらない。電界を図示する。

r,φで与えられるxy面上の点(rcosφ,rsinφ)において中心軸に対して反対方向の点(rcos(φ+π),rsin(φ+π))の電荷による電界を考えると、 両者によって電界のxy成分は打ち消される。総ての平面上の点において、同様に打ち消されるので、電界のx成分,y成分は0となる。)