I　点１（位置ベクトルＲ_１）にＱ_１〔Ｃ〕、 点２（位置ベクトルＲ_２）にＱ_２〔Ｃ〕の点電荷がある。以下の問いに答えよ。

�@　点ｒ（＝（ｘ，ｙ，ｚ））の電界を表せ。
�A　Ｒ_１＝（４，０，０）〔ｍ〕、Ｒ_２＝（０，４，０）〔ｍ〕、 Ｑ_１＝Ｑ_２＝１×１０^−８〔Ｃ〕とする。
　次の各点における電界を求めよ。（単位は〔ｍ〕） （０，０，０）、（±１，０，０）、（０，±１，０）、（±２，０，０）、（０，±２，０）、 （±１，±１，０）、（±２，±２，０）、（±３，０，０）、（０，±３，０）、（±３，±３，０）、 （±２，±１，０）、（±１，±２，０）
�B　�Aで得た電界を図示せよ。
�C　�Aで電気力線を描け。
�D　Ｒ_１＝（４，０，０）〔ｍ〕、Ｒ_２＝（０，４，０）〔ｍ〕、 Ｑ_１＝−Ｑ_２＝１×１０^−８〔Ｃ〕のとき、電気力線を描け。

解答例
�@　点電荷１，２の作る電界を足せばよい。

Ｅ ＝

Ｑ１ ４πε0

ｒ−Ｒ１ ｜ｒ−Ｒ１｜３

＋

Ｑ２ ４πε0

ｒ−Ｒ２ ｜ｒ−Ｒ２｜３

〔Ｎ／Ｃ〕

�A　�@を参考にする。１／４πε₀＝９×１０^９〔Ｆ／ｍ〕であることを考慮して、

Ｅ ＝

Ｑ１ ４πε0

（ｘ−４，ｙ，ｚ） （（ｘ−４）２＋ｙ２＋ｚ２）３／２

＋

Ｑ２ ４πε0

（ｘ，ｙ−４，ｚ） （ｘ２＋（ｙ−４）２＋ｚ２）３／２

〔Ｎ／Ｃ〕

＝ ９０

（ｘ−４，ｙ，ｚ） （（ｘ−４）２＋ｙ２＋ｚ２）３／２

＋ ９０

（ｘ，ｙ−４，ｚ） （ｘ２＋（ｙ−４）２＋ｚ２）３／２

〔Ｎ／Ｃ〕

　与えられた点に対する電界は成分で次の表のようになる。（ただし、電界の単位は〔Ｎ／Ｃ〕で、ｚ軸成分はすべての点で’０’であるから表では省略した。値を求める手続きは上の式に座標を代入するだけの単純な繰り返し計算であるので、表計算ソフトなどを利用すると簡単に値は求まる。）

点（ｘ，ｙ，ｚ）	ｘ成分	ｙ成分	：	点（ｘ，ｙ，ｚ）	ｘ成分	ｙ成分
（１，０，０）	−８．７	−５．１	：	（−１，０，０）	−４．９	−５．１
（０，１，０）	−５．１	−８．７	：	（０，−１，０）	−５．１	−４．９
（１，１，０）	−５．７	−５．７	：	（１，−１，０）	−７．９	−６．２
（−１，１，０）	−６．２	−７．９	：	（−１，−１，０）	−４．１	−４．１
（２，０，０）	−２０．５	−４．０	：	（−２，０，０）	−４．５	−４．０
（０，２，０）	−４．０	−２０．５	：	（０，−２，０）	−４．０	−４．５
（２，２，０）	０	０	：	（２，−２，０）	−７．２	−１０．１
（−２，２，０）	−１０．１	−７．２	：	（−２，−２，０）	−２．８	−２．８
（３，０，０）	−８７．８	−２．９	：	（−３，０，０）	−４．０	−２．９
（０，３，０）	２．９	−８７．８	：	（０，−３，０）	−２．９	−４．０
（３，３，０）	５．７	５．７	：	（３，−３，０）	−２．２	−１０．０
（−３，３，０）	−１０．０	−２．２	：	（−３，−３，０）	−２．０	−２．０
（２，１，０）	−１２．３	２．３	：	（２，−１，０）	−１４．９	−１０．９
（−２，１，０）	−６．２	−５．４	：	（−２，−１，０）	−３．６	−３．３
（１，２，０）	２．３	−１２．２	：	（１，−２，０）	−５．４	−６．２
（−１，２，０）	−１０．９	−１４．９	：	（−１，−２，０）	−３．３	−３．６
（０，０，０）	−５．６	−５．６

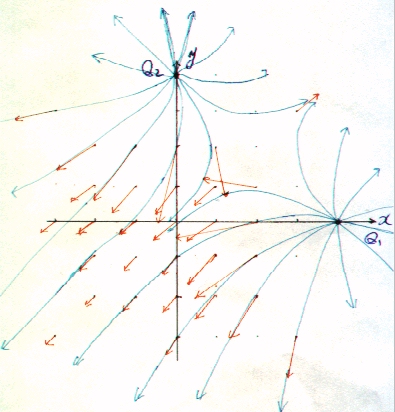
�B 上の表の電界を右図（オレンジ色）に示す。

�C　電気力線も右図（青色）に示す。電界が接線になるようになめらかに線を引く。ただし、方向は正電荷では出て、負電荷では入っていく方向。

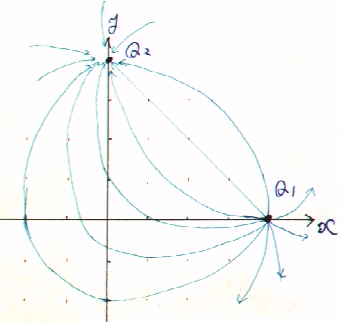
�D　�A，�Cと同様に電界を求めてつないで電気力線を表す。�Aと同じ点で、電界を求めれば下の表のようになるので、なめらかにつないで電気力線を表す。

点（ｘ，ｙ，ｚ）	ｘ成分	ｙ成分	：	点（ｘ，ｙ，ｚ）	ｘ成分	ｙ成分
（１，０，０）	−１１．３	５．１	：	（−１，０，０）	−２．３	５．１
（０，１，０）	−５．１	１１．３	：	（０，−１，０）	−５．１	２．３
（１，１，０）	−１１．４	１１．４	：	（１，−１，０）	−９．２	０．５
（−１，１，０）	−０．５	９．２	：	（−１，−１，０）	−２．７	２．７
（２，０，０）	−２４．５	４．０	：	（−２，０，０）	−０．５	４．０
（０，２，０）	−４．０	２４．５	：	（０，−２，０）	−４．０	０．５
（２，２，０）	−１５．９	１５．９	：	（２，−２，０）	−８．７	−５．８
（−２，２，０）	５．８	８．７	：	（−２，−２，０）	−１．４	１．４
（３，０，０）	−９２．２	２．９	：	（−３，０，０）	０．３	２．９
（０，３，０）	−２．９	９２．２	：	（０，−３，０）	−２．９	−０．３
（３，３，０）	−１１．４	１１．４	：	（３，−３，０）	−３．５	−７．１
（−３，３，０）	７．１	３．５	：	（−３，−３，０）	−０．８	０．８
（２，１，０）	−１９．９	１３．８	：	（２，−１，０）	−１７．３	−５．２
（−２，１，０）	−１．４	６．２	：	（−２，−１，０）	−１．２	２．５
（１，２，０）	−１３．８	１９．９	：	（１，−２，０）	−６．２	−１．４
（−１，２，０）	５．２	１７．３	：	（−１，−２，０）	−２．５	１．２
（０，０，０）	−５．６	５．６

II　半径ａ〔ｍ〕の無限長の円柱状に均一に密度ρ〔Ｃ／ｍ^３〕で電荷が分布している。以下の問いに答えよ。

�@　任意の点において、電界はどちらを向いているか。
�A　座標を適当に設定して、任意の点における電界を求めよ。
�B　�Aで求めた電界に対して、ガウスの定理の微分形が成り立つことを確認せよ。

解答例

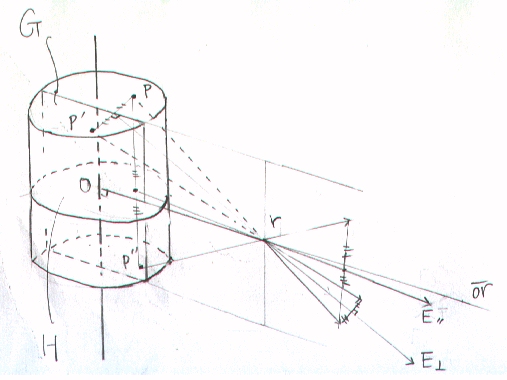
�@　電界を知りたい点をｒとし、点ｒより、円柱の中心軸に下ろした垂線の足をＯとする。 Ｏを通り、円柱の中心軸に垂直な面Ｇで、円柱を二つに分ける。
　点電荷と見なせるほど微小な領域に円柱を分けて、その内の一つの微小領域ｐが点ｒに及ぼす電界を考える。 領域ｐの面Ｇに対する対称な領域ｐ’にも同量の電荷が存在し、その電荷が点ｒに及ぼす電界は、ｐの作る電界と大きさが等しく面Ｇに対して対称である。 よって、この二つの電界を合成すると面Ｇに垂直な成分はうち消して、面Ｇ内の成分だけになる。円柱上の全電荷に対して、このような電荷の組が与えられるので、 電界は、面Ｇ内の成分のみで与えられる。 BR>　つぎに、円柱の中心軸と点ｒを含む面Ｈを考え、円柱に分布する電荷を面Ｈで二つの領域に分ける。 点電荷と見なせるほど微小な領域に円柱を分けて、その内の一つの微小領域ｐが点ｒに及ぼす電界を考える。 領域ｐの面Ｈに対する対称な領域ｐ"にも同量の電荷が存在し、その電荷が点ｒに及ぼす電界は、ｐの作る電界と大きさが等しく面Ｈに対して対称である。 よって、この二つの電界を合成すると面Ｈに垂直な成分はうち消して、面Ｈ内の成分だけになる。円柱上の全電荷に対して、このような電荷の組が与えられるので、 電界は、面Ｈ内の成分のみで与えられる。
ゆえに、点ｒにおいて、面Ｇと面Ｈに含まれる方向（円柱の中心軸に対して、垂直な方向）に電界は向く。

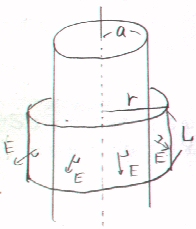
�A　円柱の中心軸から電界を知りたい点までの距離をｒとする。半径ｒ、高さＬの円柱状の閉曲面を考えて、ガウスの定理を適用する。

閉曲面上での電界をＥとすれば、

ガウスの定理の左辺＝∫Ｅ・d Ｓ（Ｓ：円柱側面＋円柱上面＋円柱下面） ＝∫Ｅ・d Ｓ（Ｓ：円柱側面）＋∫Ｅ・d Ｓ（Ｓ：円柱上面＋円柱下面）

∫Ｅ・d Ｓ（Ｓ：円柱側面）＝Ｅ∫d Ｓ（Ｓ：円柱側面） （Ｅとd Ｓは同じ方向で、Ｅは面上で同じ値）＝Ｅ２πｒＬ（側面上の電界をＥとおいた。）

∫Ｅ・d Ｓ（Ｓ：円柱上面＋円柱下面）＝０（面上でＥとd Ｓ は垂直なので内積は０）

ガウスの定理の左辺　：　Ｅ２πｒＬ

ガウスの定理の右辺　：

１ ε０

∫ρd Ｖ　＝

ρπｒ２Ｌ ε０

（ｒ＜ａ）、、

ρπａ２Ｌ ε０

（ｒ＞ａ）

ａ＜ｒ　：　Ｅ＝	ρｒ ２ε０	〔Ｎ／Ｃ〕
ａ＞ｒ　：　Ｅ＝	ρａ２ ２ε０ｒ	〔Ｎ／Ｃ〕

　円柱の中心をｚ軸とし、電界を知りたい点の座標を（ｘ，ｙ，ｚ）とおけば、ｒ＝（ｘ^２＋ｙ^２）^１／２，電界の方向は、（ｘ，ｙ，０）の方向であるから

ａ＜ｒ　：　Ｅ＝

ρ ２ε０

（ｘ，ｙ，０）　〔Ｎ／Ｃ〕

ａ＞ｒ　：　Ｅ＝

ρａ２ ２ε０

（ｘ，ｙ，０） ｘ２＋ｙ２

〔Ｎ／Ｃ〕

�B

ａ＜ｒ　：　divＥ　＝

２ρ ２ε０

＝

ρ ε０

〔Ｖ／ｍ２〕

ａ＞ｒ　：　divＥ　＝

ρａ２ ２ε０

（

２ ｘ２＋ｙ２

−

２ｘ２＋２ｙ２ （ｘ２＋ｙ２）２

）　＝０　〔Ｖ／ｍ２〕

III　厚さｔ〔ｍ〕の無限に広い板１，２が空隙ｄ〔ｍ〕で平行にある。 ただし、板１には均一に密度ρ₁〔Ｃ／ｍ^３〕の電荷が、 板２には均一に密度ρ₂〔Ｃ／ｍ^３〕の電荷がある。 また、板２から板１に向かって垂直にｚ軸を設定し、ｚ軸の原点は板２の中心にあるとする。ほかに必要な座標および座標軸は適当に設定して、以下の問いに答えよ。

�@　板１に分布する電荷による任意の点における電界の大きさと方向を求めよ。
�A　板２に分布する電荷による任意の点における電界を求めよ。
�B　板１，板２の両方に分布する電荷による任意の点における電界を求めよ。
�C　�Bにおいて、ガウスの法則の微分形が成り立つことを確認せよ。
�D　�Bにおいて、ｔ＝１〔ｍｍ〕、ｄ＝１〔ｍｍ〕、ρ_１＝ρ_２＝１×１０^−８〔Ｃ／ｍ^３〕のとき、 ｚ座標の関数として電界のｚ軸成分をグラフ化せよ。電気力線も描け。
�E　�Bにおいて、ｔ＝１〔ｍｍ〕、ｄ＝１〔ｍｍ〕、ρ_１＝−ρ_２＝１×１０^−８〔Ｃ／ｍ^３〕のとき、 ｚ座標の関数として電界のｚ軸成分をグラフ化せよ。電気力線も描け。

解答例

�@　板の厚さの中心面を基準にして、両側に等距離の点を考えると、電荷の見え方が同じであるから両地点で電界の大きさは同じである。また、電界の方向は、板に垂直（ｚ軸に並行）である。平板の中心面から両側に等距離Ｈ〔ｍ〕の面積Ｓ〔ｍ^２〕の上下面を持つ直方体状の閉曲面で、ガウスの定理を適用する。
　電界の方向を考慮して、∫Ｅ・d Ｓ＝２ＳＥ
　∫ρd Ｖ＝ρ_１Ｓ×２Ｈ　　（Ｈ＜ｔ／２）、
　　　　　　＝ρ_１Ｓ×ｔ　　（Ｈ＞ｔ／２）、

　故に電界の大きさＥは、平板から外に向かう方向を正として、

Ｈ＜

ｔ ２

：　Ｅ ＝

ρ１Ｈ ε０

〔Ｎ／Ｃ〕

Ｈ＞

ｔ ２

：　Ｅ ＝

ρ１ｔ ２ε０

〔Ｎ／Ｃ〕

　板１の厚さの中心面のは、ｚ＝ｔ＋ｄ　で与えられるので、ｚ座標を用いて表せば、Ｈ＝｜ｚ−（ｔ＋ｄ）｜である。 電界がｚ軸に平行であることを考慮して、ｚ軸の正の方向を電界の正の方向とすれば、

｜ｚ−（ｔ＋ｄ）｜＜

ｔ ２

：　Ｅ ＝

ρ１（ｚ−（ｔ＋ｄ）） ε０

〔Ｎ／Ｃ〕

｜ｚ−（ｔ＋ｄ）｜＞

ｔ ２

：　Ｅ ＝

ρ１ｔ ２ε０

（ｚ−（ｔ＋ｄ）） ｜ｚ−（ｔ＋ｄ）｜

〔Ｎ／Ｃ〕

�A　�@と同様にして電界を求める。板の厚さの中心面を基準にして、両側に等距離の点を考えると、電荷の見え方が同じであるから両地点で電界の大きさは同じである。また、電界の方向は、板に垂直（ｚ軸に並行）である。平板の中心面から両側に等距離Ｈ〔ｍ〕の面積Ｓ〔ｍ^２〕の上下面を持つ直方体状の閉曲面で、ガウスの定理を適用する。
　電界の方向を考慮して、∫Ｅ・d Ｓ＝２ＳＥ
　∫ρd Ｖ＝ρ_２Ｓ×２Ｈ　　（Ｈ＜ｔ／２）、
　　　　　　＝ρ_２Ｓ×ｔ　　（Ｈ＞ｔ／２）、

　故に電界の大きさＥは、平板から外に向かう方向を正として、

Ｈ＜

ｔ ２

：　Ｅ ＝

ρ２Ｈ ε０

〔Ｎ／Ｃ〕

Ｈ＞

ｔ ２

：　Ｅ ＝

ρ２ｔ ２ε０

〔Ｎ／Ｃ〕

　板１の厚さの中心面のは、ｚ＝０　で与えられるので、ｚ座標を用いて表せば、Ｈ＝｜ｚ｜である。 電界がｚ軸に平行であることを考慮して、ｚ軸の正の方向を電界の正の方向とすれば、

｜ｚ｜＜

ｔ ２

：　Ｅ ＝

ρ２ｚ ε０

〔Ｎ／Ｃ〕

｜ｚ｜＞

ｔ ２

：　Ｅ ＝

ρ２ｔ ２ε０

ｚ ｜ｚ｜

〔Ｎ／Ｃ〕

�B　�@と�Aの結果をまとめて、

ｚ＞ｄ＋

３ ２

ｔ　：　Ｅ ＝

ρ１ｔ ２ε０

＋

ρ２ｔ ２ε０

〔Ｎ／Ｃ〕

３ ２

ｔ

＋ｄ＞ｚ＞ｄ＋

ｔ ２

：　Ｅ ＝

ρ１（ｚ−（ｔ＋ｄ）） ε０

＋

ρ２ｔ ２ε０

〔Ｎ／Ｃ〕

ｔ ２

＜ｚ＜ｄ＋

ｔ ２

：　Ｅ ＝ −

ρ１ｔ ２ε０

＋

ρ２ｔ ２ε０

〔Ｎ／Ｃ〕

−

ｔ ２

＜ｚ＜

ｔ ２

：　Ｅ ＝ −

ρ１ｔ ２ε０

＋

ρ２ｚ ε０

〔Ｎ／Ｃ〕

ｚ＜−

ｔ ２

：　Ｅ ＝ −

ρ１ｔ ２ε０

−

ρ２ｔ ２ε０

〔Ｎ／Ｃ〕

�C　電界は、ｚ成分しかないので、ｚ座標について微分する。それぞれの領域で、ｚについて微分すれば、変数ｚの係数を求めることになる。よって、

ｚ＞ｄ＋

３ ２

ｔ　：　divＥ ＝ ０　〔Ｖ／ｍ２〕

３ ２

ｔ

＋ｄ＞ｚ＞ｄ＋

ｔ ２

：　divＥ ＝

ρ１ ε０

〔Ｖ／ｍ２〕

ｔ ２

＜ｚ＜ｄ＋

ｔ ２

：　divＥ ＝ ０　〔Ｖ／ｍ２〕

−

ｔ ２

＜ｚ＜

ｔ ２

：　divＥ ＝

ρ２ ε０

〔Ｖ／ｍ２〕

ｚ＜−

ｔ ２

：　divＥ ＝ ０　〔Ｖ／ｍ２〕

�D

ρ１ ε０

＝

ρ２ ε０

＝　１.１×１０３

であることを考慮して、グラフを描く。　グラフの例はこちら

�E　�Dと同様にして

ρ１ ε０

＝　−

ρ２ ε０

＝　１.１×１０３

であることを考慮して、グラフを描く。　グラフの例はこちら

これでこの項目は終わり

レポートの一覧へ戻る

電気磁気学I(IA:2007年度まで)へ戻る