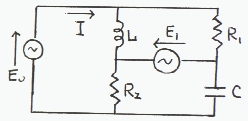
 侾丏塃偺夞楬偵偍偄偰丄俴乛俠亖俼1俼2偲偡傞丅
俬傪媮傔傛丅
侾丏塃偺夞楬偵偍偄偰丄俴乛俠亖俼1俼2偲偡傞丅
俬傪媮傔傛丅
偨偩偟丄俤0偼丄幚岠抣俤0丄妏廃攇悢冎0偺揹埑尮丄
俤1偼丄幚岠抣俤1丄妏廃攇悢冎1偺揹埑尮偱偁傞丅
丂
 侾丏塃偺夞楬偵偍偄偰丄俴乛俠亖俼1俼2偲偡傞丅
俬傪媮傔傛丅
侾丏塃偺夞楬偵偍偄偰丄俴乛俠亖俼1俼2偲偡傞丅
俬傪媮傔傛丅
偨偩偟丄俤0偼丄幚岠抣俤0丄妏廃攇悢冎0偺揹埑尮丄
俤1偼丄幚岠抣俤1丄妏廃攇悢冎1偺揹埑尮偱偁傞丅
丂
夝摎
擇偮偺揹尮偼丄妏廃攇悢偑堎側傞偺偱偦傟偧傟偺揹尮偵傛傞揹棳惉暘傪媮傔傞嵺偵偼丄
僀儞僺乕僟儞僗偑堎側傞偺偱拲堄
偙偙偱偼丄廳偹崌偣偵傛偭偰媮傔傞丅
揹尮俤0偺俬偵懳偡傞揹棳惉暘俬0偼丄揹埑尮乮偙偺応崌偵偼丄俤1乯
偺撪晹僀儞僺乕僟儞僗偑侽偱偁傞偙偲傪峫椂偟偰丄
俬0亖俤0乛乮倞冎0俴俼1乛乮倞冎0俴亄俼1乯亄俼2乛乮侾亄倞冎0俠俼2乯乯
丂丂丂亖俤0乮侾乛倞冎0俠亄俼2乯乮倞冎0俴亄俼1乯
乛乮倞冎0俴俼1乮侾乛倞冎0俠亄俼2乯亄俼2乛倞冎0俠*乮倞冎0俴亄俼1乯乯
丂丂丂亖俤0乮俼1俼2亄俴乛俠亄俼1乛倞冎0俠亄倞冎0俴俼2乯
乛乮乮俼1亄俼2乯俴乛俠亄俼1俼2乮倞冎0俴亄侾乛倞冎0俠乯乯
丂丂丂亖俤0乮俀亄俼1乛倞冎0俴亄倞冎0俠俼2乯
乛乮俼1亄俼2亄倞乮冎0俴亅侾乛冎0俠乯乯
揹尮俤1偺俬偵懳偡傞揹棳惉暘俬1偼丄俼2傪棳傟傞揹棳偲俠傪棳傟傞揹棳偺嵎偱梌偊傜傟傞丅
揹埑尮乮偙偺応崌偵偼丄俤0乯偺撪晹僀儞僺乕僟儞僗偑侽偱偁傞偙偲傪峫椂偡傟偽丄俤1偐傜棳傟傞揹棳傪俬11偲偟偰
俬1亖俬11乮倞冎1俴乛乮倞冎1俴亄俼2乯亅俼1乛乮侾乛倞冎1俠亄俼1乯乯
丂丂丂亖俬11乮乮倞冎1俴乮侾乛倞冎1俠亄俼1乯亅俼1乮倞冎1俴亄俼2乯乯乛乮倞冎1俴亄俼2乯乮侾乛倞冎1俠亄俼1乯乯
丂丂丂亖俬11乮俴乛俠亅俼1俼2乯乯乛乮倞冎1俴亄俼2乯乮侾乛倞冎1俠亄俼1乯乯
丂丂丂亖侽丂乮俴乛俠亅俼1俼2亖侽偺忦審傛傝乯
丂乮揹尮俤1偐傜尒偨僽儕僢僕偺暯峵忦審偐傜丄俬1亖侽偼帺柧乯
丂俬亖俬0亄俬1亖俬0
丂丂亖俤0乮俼1俼2亄俴乛俠亄俼1乛倞冎0俠亄倞冎0俴俼2乯
乛乮乮俼1亄俼2乯俴乛俠亄俼1俼2乮倞冎0俴亄侾乛倞冎0俠乯乯
丂
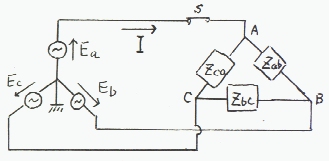 俀丏塃偺夞楬偵偍偄偰丄埲壓偺栤偄偵摎偊傛丅
俀丏塃偺夞楬偵偍偄偰丄埲壓偺栤偄偵摎偊傛丅
揹尮偼丄幚岠抣俤偺懳徧嶰憡岎棳揹尮偲偡傞丅
嘆倎憡傪婎弨偲偟偰丄俬傪媮傔傛丅
夝摎
俙仺俛偵棳傟傞揹棳傪俬AB丄俠仺俙偵棳傟傞揹棳傪俬CA偲偡傟偽丄
俬亖俬AB亅俬CA偱梌偊傜傟傞丅
俬AB亖乮俤a亅俤b乯乛倅ab亖俁1/2倕j兾/6俤a乛倅ab
俬CA亖乮俤c亅俤a乯乛倅ca亖俁1/2倕j5兾/6俤a乛倅ca
俬亖俬AB亅俬CA亖俁1/2倕j兾/6俤a乮侾乛倅ab亅倕j2兾/3乛倅ca乯
嘇俽傪奐偄偨帪丄揰俙偱偺懳抧揹埵傪媮傔傛丅
夝摎
揰俠偐傜應偭偨揰俙偺揹埵倁CA偼丄俛俠娫偵俤b亅俤c偺揹埑偑報壛偝傟偰偄傞偙偲傪峫椂偟偰丄
倁CA亖乮俤b亅俤c乯倅ca乛乮倅bc亄倅ca乯
揰俠偺懳抧揹埵偼丄俤c偱偁傞偐傜丄揰俙偺懳抧揹埵倁a偼丄
倁a亖俤c亄倁CA亖俤c亄乮俤b亅俤c乯倅ca乛乮倅bc亄倅ca乯
丂丂丂丂亖乮俤b倅ca亄俤c倅bc乯乛乮倅bc亄倅ca乯
丂
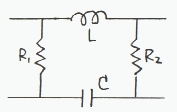 俁丏塃偺夞楬偵偍偄偰丄巐抂巕掕悢傪媮傔傛丅
俁丏塃偺夞楬偵偍偄偰丄巐抂巕掕悢傪媮傔傛丅
夝摎
倁1亖俙倁2亄俛俬2
俬1亖俠倁2亄俢俬2
偵偍偄偰丄俙乣俢傪媮傔傟偽傛偄丅忋偺幃傛傝丄
俙亖倁1乛倁2乮俬2亖侽丗塃懁傪奐曻乯
俛亖倁1乛俬2乮倁2亖侽丗塃懁傪抁棈乯
俠亖俬1乛倁2乮俬2亖侽丗塃懁傪奐曻乯
俢亖俬1乛俬2乮倁2亖侽丗塃懁傪抁棈乯
偱媮傔傞偙偲偑偱偒傞丅嵍懁偺抂巕偵揔摉側揹尮乮椺偊偽丄幚岠抣俤丄妏廃攇悢冎偺揹埑尮乯
傪憐掕偟偰丄忋偺斾傪媮傔傞丅偮傑傝丄倁1亖俤偲偟偰峫偊傞丅
俙偵偮偄偰丗丂捈楍僀儞僺乕僟儞僗偱偺暘埑偱偁傞
倁2亖俤俼2乛乮俼2亄倞乮冎俴亅侾乛冎俠乯乯
俙亖俤乛倁2亖侾亄倞乮冎俴亅侾乛冎俠乯乛俼2
俛偵偮偄偰丗丂俴俠偵棳傟傞揹棳偱偁傞
俬2亖俤乛倞乮冎俴亅侾乛冎俠乯
俛亖俤乛俬2亖倞乮冎俴亅侾乛冎俠乯
俠偵偮偄偰丗丂俤傛傝棳傟傞慡揹棳偲俼2偺揹埑偺斾偱偁傞
慡揹棳俬1亖俤乮侾乛俼1亄侾乛乮俼2亄倞乮冎俴亅侾乛冎俠乯乯乯
倁2亖俤俼2乛乮俼2亄倞乮冎俴亅侾乛冎俠乯乯
俠亖俬1乛倁2亖乮侾乛俼1亄侾乛乮俼2亄倞乮冎俴亅侾乛冎俠乯乯乯乛俼2乛乮俼2亄倞乮冎俴亅侾乛冎俠乯乯
丂丂亖乮俼2亄倞乮冎俴亅侾乛冎俠乯乯乛俼1俼2亄侾乛俼2
丂丂亖侾乛俼1亄侾乛俼2亄倞乮冎俴亅侾乛冎俠乯乛俼1俼2
俢偵偮偄偰丗丂慡揹棳偵懳偡傞俴俠偵棳傟傞揹棳偺妱崌偱偁傞
俬2亖俤乛倞乮冎俴亅侾乛冎俠乯
俬1亖俤乮侾乛俼1亄侾乛倞乮冎俴亅侾乛冎俠乯乯
俢亖俬1乛俬2亖侾亄倞乮冎俴亅侾乛冎俠乯乛俼1
丂
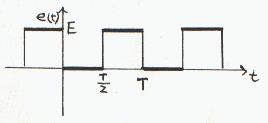 係丏塃偺廃婜俿偺揹埑攇宍倕乮倲乯傪僼乕儕僄暘夝偣傛丅
係丏塃偺廃婜俿偺揹埑攇宍倕乮倲乯傪僼乕儕僄暘夝偣傛丅
夝摎
捈棳惉暘俤0亖侾乛俿仏佺倕乮倲乯倓倲丟乮倲丗侽乣俿乯
丂丂丂丂亖侾乛俿仏佺俤倓倲丟乮倲丗俿乛俀乣俿乯亖俤俿乛俀乛俿亖俤乛俀
捈棳惉暘傪彍偄偨娭悢乪倕乮倲乯亅俤乛俀乫偼丄婏娭悢偱偁傞偐傜倱倝値惉暘偩偗傪峫偊傟偽傛偄丅
値師偺學悢俤sn亖俀乛俿仏佺倱倝値乮値冎倲乯倕乮倲乯倓倲丟乮倲丗侽乣俿乯偱偁傞偐傜
俤sn亖俀乛俿仏佺俤倱倝値乮値冎倲乯倓倲丟乮倲丗俿乛俀乣俿乯
丂丂丂亖俀俤乛俿仏乵亅侾乛値冎仏們倧倱乮値冎倲乯乶丟乮倲丗俿乛俀乣俿乯
丂丂丂亖亅俀俤乛値冎俿仏乮們倧倱乮値冎俿乯亅們倧倱乮値冎俿乛俀乯乯
丂丂丂亖亅俀俤乛値冎俿仏乮侾亅乮亅侾乯n乯
丂値偑婏悢偺帪偺傒侽偱側偄抣偵側傞丅偙偺偲偒丄
俤sn亖亅俀俤乛兾値
倕乮倲乯亖俤乮侾乛俀亅俀乛兾仏儼侾乛値仏倱倝値乮値冎倲乯乯丟乮値丗惓偺婏悢乯丂