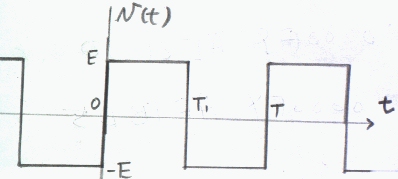

塃偵帵偝傟傞傛偆側曽宍偺廃婜俿偺揹埑倁乮倲乯偑偁傞丅埲壓偵偮偄偰峫偊傞丅
嘆丂俿1亖俿乛俀偺偲偒丄倁乮倲乯傪僼乕儕僄曄姺乮惓尫攇偱暘夝乯偡傞丅
倁乮倲乯亖亅倁乮亅倲乯傛傝丄偙偺揹埑攇宍偼婏娭悢偱偁傞丅傛偭偰丄冎亖俀兾乛俿偲偟偰丄
丂倁乮倲乯亖儼倁n倱倝値乮値冎倲乯丟乮値丗帺慠悢乯
偲偐偗傞丅
丂倁n亖俀乛俿丒佺乮倁乮倲乯倱倝値乮値冎倲乯乯倓倲丟乮倲丗侽乣俿乯
丂丂丂丂亖俀乛俿丒乮佺乮俤倱倝値乮値冎倲乯乯倓倲丟乮倲丗侽乣俿1乯亄佺乮亅俤倱倝値乮値冎倲乯乯倓倲丟乮倲丗俿1乣俿乯乯
丂丂丂丂亖俀俤乛俿丒乮乵侾乛値冎丒乮亅們倧倱乮値冎倲乯乯乶丟乮倲丗侽乣俿乛俀乯亅乵侾乛値冎丒乮亅們倧倱乮値冎倲乯乯乶丟乮倲丗俿乛俀乣俿乯乯
丂丂丂丂亖俀俤乛値冎俿丒乮乮侾亅們倧倱乮値冎俿乛俀乯乯亅乮亅們倧倱乮値冎俿乯亄們倧倱乮値冎俿乛俀乯乯乯
丂丂丂丂亖俀俤乛値俀兾丒乮乮侾亅們倧倱乮値兾乯乯亅乮亅們倧倱乮俀兾値乯亄們倧倱乮値兾乯乯乯
丂丂丂丂亖俀俤乛値兾丒乮侾亅乮亅侾乯n乯
丂値丟婏悢丂倁n亖係俤乛値兾丄丂値丟嬼悢丂倁n亖侽丂偲側傞丅幃偱昞偣偽丄
丂倁乮倲乯亖係俤乛兾儼侾乛値丒倱倝値乮値冎倲乯丟乮値丗惓偺婏悢乯
丂丂丂丂丂亖係俤乛兾丒乮倱倝値乮冎倲乯亄侾乛俁丒倱倝値乮俁冎倲乯亄侾乛俆丒倱倝値乮俆冎倲乯亄侾乛俈丒倱倝値乮俈冎倲乯亄丒丒丒乯
丂
嘇丂嘆偵偍偄偰倁乮倲乯偺幚岠抣|倁|傪媮傔傞丅
丂|倁|2亖侾乛俿丒佺倁乮倲乯2倓倲丟乮倲丗侽乣俿乯
丂丂丂丂丂丂丂丂亖侾乛俿丒乮佺俤2倓倲丟乮倲丗侽乣俿乛俀乯亄佺乮亅俤乯2倓倲丟乮倲丗俿乛俀乣俿乯乯
丂丂丂丂丂丂丂丂亖俤2
傛偭偰丄
|倁|亖俤
暿夝丂僼乕儕僄媺悢揥奐偟偨寢壥傪巊偊偽丄
丂|倁|2亖乮係俤乛兾乯2儼乮侾乛値乯2乛俀丟乮値丗惓偺婏悢乯
丂丂丂丂丂亖俉乮俤乛兾乯2丒乮侾亄侾乛俁2亄侾乛俆2亄侾乛俈2亄丒丒丒乯
傛偭偰丄
|倁|亖乮係俤乛兾嚂俀乯丒嚂乮侾亄侾乛俁2亄侾乛俆2亄侾乛俈2亄丒丒丒乯
僆儅働丂忋偺擇偮偺|倁|2偼摨偠抣偱偁傞偐傜丄
丂侾亄侾乛俁2亄侾乛俆2亄侾乛俈2亄丒丒丒亖兾2乛俉
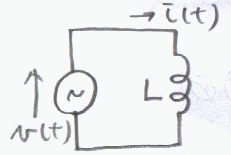
嘊丂嘆偺揹埑偑塃偺夞楬偵報壛偝傟偨帪丄倝乮倲乯傪媮傔傞丅偨偩偟丄倝乮侽乯亖侽
丂倁乮倲乯亖俴倓倝乮倲乯乛倓倲丂丄倝乮侽乯亖侽側偺偱丄倲亖冄偵偍偗傞揹棳倝乮冄乯偼丄
丂倝乮冄乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄乯丂偱摼傜傟傞丅
丂侽亙冄亙俿乛俀偺偲偒
丂倝乮冄乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄乯
丂丂丂丂亖侾乛俴丒佺俤倓倲丟乮倲丗侽乣冄乯
丂丂丂丂亖俤乛俴丒冄
丂俿乛俀亙冄亙俿偺偲偒
丂倝乮冄乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄乯
丂丂丂丂亖侾乛俴丒乮佺俤倓倲丟乮倲丗侽乣俿乛俀乯亄佺亅俤倓倲丟乮倲丗俿乛俀乣冄乯乯
丂丂丂丂亖侾乛俴丒乮俤俿乛俀亅俤乮冄亅俿乛俀乯乯
丂丂丂丂亖俤乛俴丒乮俿亅冄乯
丂俿偩偗帪娫傪偢傜偣偨帪偺揹棳倝乮冄亄俿乯偵偮偄偰峫偊傞丅
丂侽亙冄亙俿乛俀偺偲偒
丂倝乮冄亄俿乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄亄俿乯
丂丂丂丂亖侾乛俴丒乮佺倁乮倲乯倓倲丟乮倲丗侽乣俿乯亄佺倁乮倲乯倓倲丟乮倲丗俿乣冄亄俿乯乯
丂丂丂丂亖倝乮俿乯亄侾乛俴丒佺俤倓倲丟乮倲丗俿乣冄亄俿乯乯
丂丂丂丂亖俤乛俴丒冄丂乮偡偖慜偱媮傔偨傛偆偵丄倝乮俿乯亖侽乯
丂丂丂丂亖倝乮冄乯
丂俿乛俀亙冄亙俿偺偲偒
丂倝乮冄亄俿乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄亄俿乯
丂丂丂丂亖侾乛俴丒乮佺倁乮倲乯倓倲丟乮倲丗侽乣俿亄俿乛俀乯亄佺倁乮倲乯倓倲丟乮倲丗俿亄俿乛俀乣冄亄俿乯乯
丂丂丂丂亖倝乮俿亄俿乛俀乯亄侾乛俴丒佺亅俤倓倲丟乮倲丗俿亄俿乛俀乣冄亄俿乯乯
丂丂丂丂亖俤乛俴丒俿乛俀亅俤乛俴丒乮冄亅俿乛俀乯丂乮偡偖慜偱媮傔偨傛偆偵丄倝乮俿亄俿乛俀乯亖倝乮俿乛俀乯亖俤乛俴丒俿乛俀乯
丂丂丂丂亖俤乛俴丒乮俿亅冄乯
丂丂丂丂亖倝乮冄乯
丂偙傟傪孞傝曉偣偽丄倝乮冄亄値俿乯亖倝乮冄乯丄倝乮冄乯偼廃婜俿偺娭悢偱偁傞偙偲偑暘偐傞丅
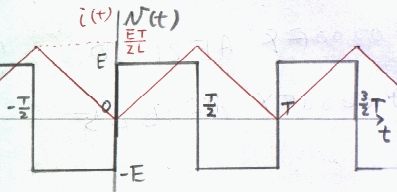
偙傟傪恾帵偡傟偽丄塃偺僌儔僼偺愒慄偺傛偆偵側傞丅
暿夝丂僼乕儕僄媺悢揥奐偟偨寢壥傪巊偊偽丄
丂倝乮冄乯亖侾乛俴丒佺倁乮倲乯倓倲丟乮倲丗侽乣冄乯
丂丂丂丂丂亖侾乛俴丒佺乮係俤乛兾儼侾乛値丒倱倝値乮値冎倲乯丟乮値丗惓偺婏悢乯乯倓倲丟乮倲丗侽乣冄乯
丂丂丂丂丂亖係俤乛兾俴丒儼佺乮侾乛値丒倱倝値乮値冎倲乯乯倓倲丟乮倲丗侽乣冄乯丟乮値丗惓偺婏悢乯乯
丂丂丂丂丂亖係俤乛兾俴丒儼乵亅侾乛値丒侾乛値冎丒們倧倱乮値冎倲乯乶丟乮倲丗侽乣冄乯丟乮値丗惓偺婏悢乯乯
丂丂丂丂丂亖係俤乛兾俴丒儼亅侾乛値2冎丒乮們倧倱乮値冎冄乯亅侾乯丟乮値丗惓偺婏悢乯
丂丂丂丂丂亖係俤乛兾冎俴丒儼侾乛値2丒乮侾亅們倧倱乮値冎冄乯乯丟乮値丗惓偺婏悢乯
丂丂丂丂丂亖俀俤俿乛兾2俴丒儼侾乛値2丒乮侾亅們倧倱乮値冎冄乯乯丟乮値丗惓偺婏悢乯
儼侾乛値2丟乮値丗惓偺婏悢乯亖兾2乛俉傪巊偊偽丄
丂倝乮冄乯亖俤俿乛係俴亅俀俤俿乛兾2俴丒儼侾乛値2丒們倧倱乮値冎冄乯丟乮値丗惓偺婏悢乯
僆儅働愭偵媮傔偨揹棳傪僼乕儕僄媺悢暘夝偡傞偲忋偺幃偵側傞偼偢偱偁傞丅乮妋偐傔傞乯
倝乮冄乯偼丄倝乮冄乯亖倝乮亅冄乯傛傝丄嬼娭悢偱偁傞丅傛偭偰丄師偺傛偆偵揥奐偝傟傞丅
倝乮冄乯亖倝0亄儼倝n們倧倱乮値冎冄乯丟乮値丗帺慠悢乯
丂丂丂倝0亖侾乛俿丒佺倝乮冄乯們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乯
丂丂丂倝n亖俀乛俿丒佺倝乮冄乯們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乯
丂丂丂倝n亖俀乛俿丒乮佺俤乛俴丒冄們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乛俀乯亄佺俤乛俴丒乮俿亅冄乯們倧倱乮値冎冄乯倓冄丟乮冄丗俿乛俀乣俿乯乯
戞俀崁偵偍偄偰丄俿亅冄亖倲偲抲偗偽丄
佺俤乛俴丒乮俿亅冄乯們倧倱乮値冎冄乯倓冄丟乮冄丗俿乛俀乣俿乯亖佺俤乛俴丒倲們倧倱乮値冎乮俿亅倲乯乯倓倲丟乮倲丗侽乣俿乛俀乯
丂丂丂丂丂丂丂丂亖佺俤乛俴丒倲們倧倱乮値冎乮倲亅俿乯倓倲丟乮倲丗侽乣俿乛俀乯
丂丂丂丂丂丂丂丂亖佺俤乛俴丒倲們倧倱乮値冎倲亅値冎俿乯倓倲丟乮倲丗侽乣俿乛俀乯
丂丂丂丂丂丂丂丂亖佺俤乛俴丒倲們倧倱乮値冎倲乯倓倲丟乮倲丗侽乣俿乛俀乯丂乮値冎俿亖俀兾値側偺偱乯
丂備偊偵丄戞俀崁偼丄戞侾崁偲摨偠抣偵側傞丅傛偭偰丄
丂丂丂倝n亖俀乛俿丒乮俀佺俤乛俴丒冄們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乛俀乯乯
丂丂丂丂丂丂丂亖係俤乛俿俴丒乮佺丒冄們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乛俀乯乯
丂丂丂丂丂丂丂亖係俤乛俿俴丒乮乵冄乛値冎丒倱倝値乮値冎冄乯乶丟乮冄丗侽乣俿乛俀乯亅佺侾乛値冎丒倱倝値乮値冎冄乯倓冄丟乮冄丗侽乣俿乛俀乯乯
丂丂丂丂丂丂丂亖係俤乛俿俴丒乮亅侾乛乮値冎乯2丒乵亅們倧倱乮値冎冄乯乶丟乮冄丗侽乣俿乛俀乯乯丂乮戞侾崁偼侽偵側傞乯
丂丂丂丂丂丂丂亖係俤乛俿俴乮値冎乯2丒乮們倧倱乮値兾乯亅侾乯
丂丂丂丂丂丂丂亖俤俿乛俴乮兾値乯2丒乮們倧倱乮値兾乯亅侾乯
丂丂丂丂丂丂丂亖亅俀俤俿乛俴乮兾値乯2丟乮値丗婏悢乯丄丂侽丟乮値丗嬼悢乯丂
丂倝0亖侾乛俿丒佺倝乮冄乯們倧倱乮値冎冄乯倓冄丟乮冄丗侽乣俿乯
丂丂丂丂丂丂丂亖侾乛俿丒乮佺俤乛俴丒冄倓冄丟乮冄丗侽乣俿乛俀乯亄佺俤乛俴丒乮俿亅冄乯倓冄丟乮冄丗俿乛俀乣俿乯乯
丂丂丂丂丂丂丂亖俤乛俿俴丒乮乵侾乛俀丒冄2乶丟乮冄丗侽乣俿乛俀乯亄乵俿冄亅侾乛俀丒冄2乶丟乮冄丗俿乛俀乣俿乯乯
丂丂丂丂丂丂丂亖俤乛俿俴丒乮侾乛俀丒乮俿乛俀乯2乯亄乮俿俿亅侾乛俀丒俿2乯亅乮俿俿乛俀亅侾乛俀丒乮俿乛俀乯2乯乯
丂丂丂丂丂丂丂亖俤俿乛係俴
丂愭掱偺暿夝偲堦抳偡傞丅乮摨偠検傪堘偆昞尰偱昞偟偨偩偗偺偙偲偱偁傞乯
嘋丂侽亙俿1亙俿偺偲偒倁乮倲乯傪僼乕儕僄暘夝偡傞丅
丂倁乮倲乯亖倁0亄儼乮倁sn倱倝値乮値冎倲乯亄倁cn們倧倱乮値冎倲乯乯丟乮値丗帺慠悢乯
丂丂倁0亖侾乛俿丒佺倁乮倲乯倓倲丟乮倲丗侽乣俿乯
丂丂丂丂丂亖侾乛俿丒乮佺俤倓倲丟乮倲丗侽乣俿1乯亅佺俤倓倲丟乮倲丗俿1乣俿乯
丂丂丂丂丂亖侾乛俿丒乮俤俿1亄俤乮俿1亅俿乯乯
丂丂丂丂丂亖俤乮俀俿1乛俿亅侾乯
丂丂倁sn亖俀乛俿丒佺乮倁乮倲乯倱倝値乮値冎倲乯乯倓倲丟乮倲丗侽乣俿乯
丂丂丂丂亖俀乛俿丒乮佺乮俤倱倝値乮値冎倲乯乯倓倲丟乮倲丗侽乣俿1乯亄佺乮亅俤倱倝値乮値冎倲乯乯倓倲丟乮倲丗俿1乣俿乯乯
丂丂丂丂亖俀俤乛俿丒乮乵亅侾乛値冎丒們倧倱乮値冎倲乯乶丟乮倲丗侽乣俿1乯亄乵侾乛値冎丒們倧倱乮値冎倲乯乶丟乮倲丗俿1乣俿乯乯
丂丂丂丂亖俀俤乛俿丒乮侾乛値冎丒乮侾亅們倧倱乮値冎俿1乯乯亄侾乛値冎丒乮們倧倱乮値冎俿乯亅們倧倱乮値冎俿1乯乯乯
丂丂丂丂亖俀俤乛値冎俿丒乮侾亅們倧倱乮値冎俿1乯亄侾亅們倧倱乮値冎俿1乯乯
丂丂丂丂亖俀俤乛値兾丒乮侾亅們倧倱乮値冎俿1乯乯
丂丂倁cn亖俀乛俿丒佺乮倁乮倲乯們倧倱乮値冎倲乯乯倓倲丟乮倲丗侽乣俿乯
丂丂丂丂亖俀乛俿丒乮佺乮俤們倧倱乮値冎倲乯乯倓倲丟乮倲丗侽乣俿1乯亄佺乮亅俤們倧倱乮値冎倲乯乯倓倲丟乮倲丗俿1乣俿乯乯
丂丂丂丂亖俀俤乛俿丒乮乵侾乛値冎丒倱倝値乮値冎倲乯乶丟乮倲丗侽乣俿1乯亅乵侾乛値冎丒倱倝値乮値冎倲乯乶丟乮倲丗俿1乣俿乯乯
丂丂丂丂亖俀俤乛俿丒乮侾乛値冎丒倱倝値乮値冎俿1乯乯亅侾乛値冎丒乮倱倝値乮値冎俿乯亅倱倝値乮値冎俿1乯乯乯
丂丂丂丂亖俀俤乛値冎俿丒乮倱倝値乮値冎俿1乯乯亅乮亅倱倝値乮値冎俿1乯乯乯
丂丂丂丂亖俀俤乛値兾丒倱倝値乮値冎俿1乯
丂偙傟傜偺學悢傪梡偄偰
丂丂倁乮倲乯亖俤乮俀俿1乛俿亅侾亄
儼俀乛値兾仏乮乮侾亅們倧倱乮値冎俿1乯乯倱倝値乮値冎倲乯亄倱倝値乮値冎俿1乯們倧倱乮値冎倲乯乯丟乮値丗帺慠悢乯乯