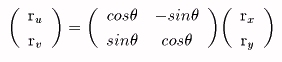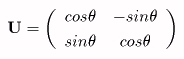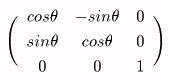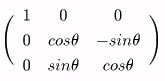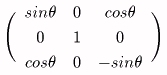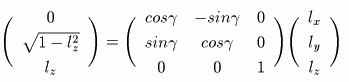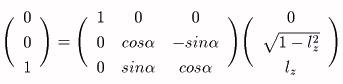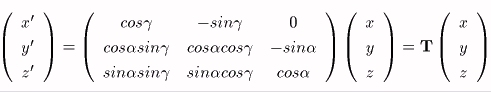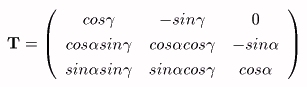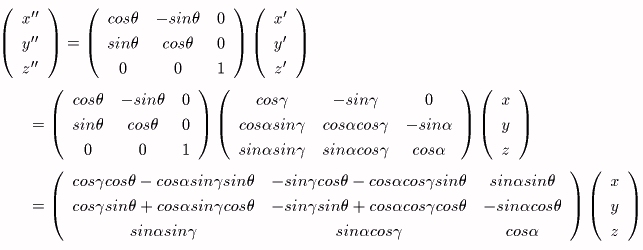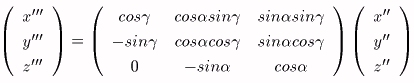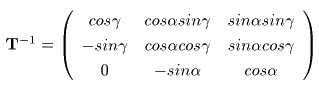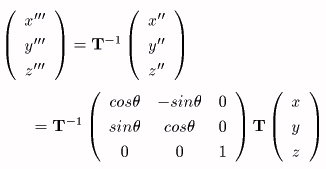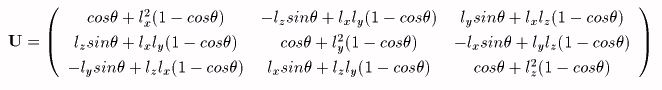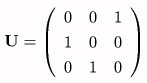偙偺儁乕僕偼丄
Monday, 21-May-2007 21:10:28 JST偵峏怴偝傟傑偟偨丅
偙偺儁乕僕偼丄乫屻摗 塸梇仐揹婥僔僗僥儉岺妛壢丂拞晹戝妛乫偑嶌惉偟偰偄傑偡丅
楢棈偼丄屻摗仐揹婥僔僗僥儉岺妛壢傊偍婅偄偟傑偡丅
丂揹婥岺妛偱巊偆悢妛揑庤朄 presented since 1996
揰乮儀僋僩儖乯偺夞揮曄姺
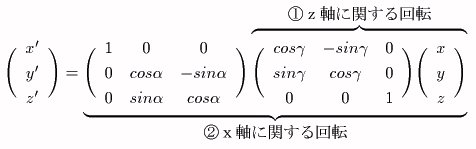
擇師尦暯柺偱偺夞揮丂亅丂峴楍昞尰丄嶰妏娭悢偺榓愊偺娭學乮岞幃乯
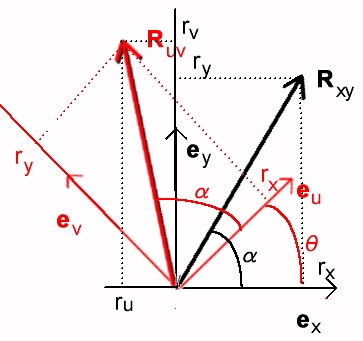
丂倶倷暯柺忋偺擟堄偺揰俼xy乮俼xy亖乮倰x丆倰y乯乯傪
尨揰傪拞怱偲偟偰兤夞揮偝偣偨揰偺嵗昗俼uv乮俼uv亖乮倰u丆倰v乯乯傪峫偊傞丅
揰俼xy偺尨揰偐傜偺嫍棧傪倰丄慄暘俷俼xy偺倶幉偐傜倷幉偵岦偐偭偰應偭偨倶幉偲偺側偡妏傪兛偲偍偗偽丄
倰x亖倰們倧倱兛丄倰y亖倰倱倝値兛偱梌偊傜傟傞丅
嵗昗偵懳墳偡傞扨埵儀僋僩儖偱昞偣偽丄倶倷嵗昗偵懳墳偡傞扨埵儀僋僩儖傪倕x丄倕y偲偍偄偰丄
丂俼xy亖倰x倕x亄倰y倕y
偲昞偝傟傞丅傑偨丄乮倕u丄倕v丄倕x丄倕y偼乮嵗昗偺曽岦傪昞偡扨埵儀僋僩儖偲偄偆偩偗偱側偔乯嵗昗偱昞偝傟傞偲偄偆堄枴偱丄儀僋僩儖偺曄姺偵懳偟偰俼xy偲摨偠偵埖偭偰傛偄偺偱丄乯倕倶丄倕倷傪俼xy偲摨條偵兤夞揮偝偣偨儀僋僩儖傪倕倳丄倕倴偲偍偗偽丄俼xy丄倕x丄倕y偲摨條偺娭學偑偁傞偺偱丄
丂俼uv亖倰x倕u亄倰y倕v
偲昞偝傟傞丅恾傪嶲峫偵偟偰丄倕u丄倕v傪倕x丄倕y偱昞偣偽丄
丂倕u亖們倧倱兤倕x亄倱倝値兤倕y丄倕v亖亅倱倝値兤倕x亄們倧倱兤倕y
偱偁傞偙偲偑暘偐傞丅恾傛傝丄
俼uv亖倰x倕u亄倰y倕v
丂丂亖倰x乮們倧倱兤倕x亄倱倝値兤倕y乯亄倰y乮亅倱倝値兤倕x亄們倧倱兤倕y乯
丂丂亖倰u倕x亄倰v倕y
倕倶丄倕倷偵偐偐傞學悢傪斾妑偡傟偽丄
倰u亖們倧倱兤倰x亅倱倝値兤倰y亖倰乮們倧倱兤們倧倱兛亅倱倝値兤倱倝値兛乯
倰v亖倱倝値兤倰x亄們倧倱兤倰y亖倰乮們倧倱兤倱倝値兛亄倱倝値兤們倧倱兛乯
曄姺峴楍倀偵傛偭偰丄倶倷嵗昗偱昞尰偝傟傞乮倰u丆倰v乯偲乮倰x丆倰y乯偺娭學偼
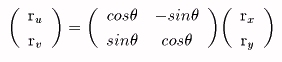
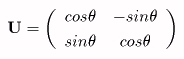
偺傛偆偵昞尰偝傟傞丅
丂恾傛傝丄倰u亖倰們倧倱乮兛亄兤乯丄倰v亖倰倱倝値乮兛亄兤乯偲昞偡偙偲偑壜擻偱偁傞丅備偊偵丄
倰u亖倰乮們倧倱兤們倧倱兛亅倱倝値兤倱倝値兛乯亖倰們倧倱乮兛亄兤乯
倰v亖倰乮們倧倱兤倱倝値兛亄倱倝値兤們倧倱兛乯亖倰倱倝値乮兛亄兤乯
側傞娭學偑偁傞偙偲偑暘偐傞丅師偺傛偆側嶰妏娭悢偺榓愊偺娭學乮岞幃乯偑摫偐傟傞丅
們倧倱乮兛亄兤乯亖們倧倱兤們倧倱兛亅倱倝値兤倱倝値兛
倱倝値乮兛亄兤乯亖們倧倱兤倱倝値兛亄倱倝値兤們倧倱兛
倕u偼丄倕x乮亖乮侾丆侽乯乯傪兤夞揮丄倕v偼丄倕y乮亖乮侽丆侾乯乯傪兤夞揮偝偣偰摼傜傟傞偙偲偐傜揰傪昞偡儀僋僩儖昞尰偵偍偄偰丄埵抲傪昞偡儀僋僩儖偺學悢偼曄偊偢偵丄嵗昗偵懳墳偡傞儀僋僩儖偩偗曄姺偡傟偽丄揰偺夞揮偑摼傜傟傞偙偲偑暘偐傞丅
乮儊儕乕僑乕儔儞僪偺栘攏偵忔偭偰偄傞恖偼儊儕乕僑乕儔儞僪偺夞揮乮嵗昗偵懳墳偡傞儀僋僩儖偺夞揮乯偲偲傕偵堏摦偡傞丅栘攏偲偺埵抲娭學乮嵗昗偵懳墳偡傞儀僋僩儖偵偐偐傞'埵抲傪昞偡偨傔偺學悢'乯偼曄傢傜側偄丅乯
倕u偺曽岦偵倳幉傪丄倕v偺曽岦偵倴幉傪愝掕偟偨偙偲偵憡摉偡傞丅乮倳幉偼倶幉傪兤夞揮丄倴幉偼倷幉傪兤夞揮偝偣偰摼傜傟傞丅乮倶倷暯柺傪倸幉偺廃傝偱兤夞揮偝偣偨偺偑倳倴嵗昗乯倳倴嵗昗偱偼丄倶倷嵗昗偺応崌偲摨偠惉暘偲偟偰揰偑梌偊傜傟傞丅乯
偡傋偰偺揰偑丄尨揰偵懳偟偰摨偠偩偗乮兤偩偗乯夞揮偝傟傞偺偱丄揰偺廤崌偑偁傞恾宍傪梌偊偰偄傟偽丄夞揮屻偺恾宍偼夞揮慜偲崌摨偱偁傞丅
暋悢偺儀僋僩儖傪夞揮偝偣偰傕丄儀僋僩儖憡屳偺娭學偼晄曄偱偁傞丅乮儊儕乕僑乕儔儞僪偵忔偭偰挱傔傟偽丄栘攏偺埵抲偼晄曄偱偁傞丅乯
嶰師尦嬻娫偱偺夞揮
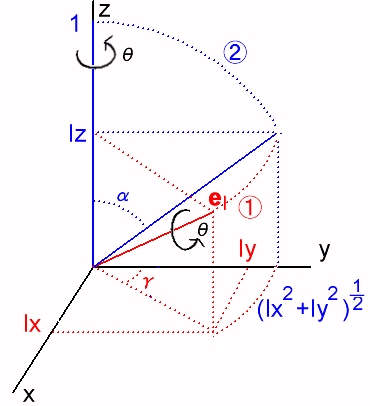
丂倶倷倸嬻娫偵偍偗傞尨揰傪捠傞捈慄傪幉偵偟偨夞揮偵偮偄偰峫偊傞丅
愭偵峫偊偨倶倷暯柺偵偍偗傞夞揮傪嶰師尦偵奼挘偡傞偲丄倶倷暯柺偵偍偗傞夞揮偼丄倸幉偺惓偺曽岦偐傜尨揰傪挱傔偨偲偒偺倶倷暯柺偵幩塭偝傟傞揰偺夞揮偵憡摉偡傞丅偡側傢偪丄倸幉偺惓偺曽岦偐傜尨揰傪挱傔偨偲偒丄倸幉傪夞揮幉偲偟偰嵍夞傝偵夞揮偝偣傞乮尨揰偐傜倸幉偺惓偺曽岦傪挱傔偨偲偒塃夞傝偵夞揮偝偣傞乯偙偲偵側傞丅
倸幉偺廃傝偺兤夞揮傪昞偡峴楍
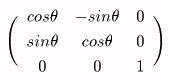
摨條偵倶幉丄倷幉偺廃傝偺夞揮傪峫偊傞偲丄
倶幉廃傝偺兤夞揮傪昞偡峴楍
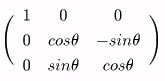
倷幉廃傝偺兤夞揮傪昞偡峴楍
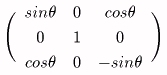
丂偙傟傜偺曄姺偼丄夞揮偱偁傞偺偱儀僋僩儖憡屳偺娭學偼曄傢傜側偄丅堦斒偵丄倕l乮亖乮倢x丄倢y丄倢z乯
丂乮扨埵儀僋僩儖偱偁傞偐傜丄倢x2亄倢y2亄倢z2亖侾乯偺幉偺廃傝偺兤夞揮傪峫偊傞応崌偵偼丄倕l傪偳傟偐偺嵗昗幉偵堦抳偝偣傟偽丄夞揮傪婰弎偡傞偙偲偑偱偒傞丅師偺庤弴偱夞揮傪昞偡峴楍傪媮傔傞丅
嘆倸幉偱夞揮偝偣偰丄倕l傪倷倸暯柺偵堏摦偝偣傞丅乮夞揮妏傪兞偲偡傞乯
嘇倶幉偱夞揮偝偣偰丄倕l傪倸幉偲堦抳偝偣傞丅乮夞揮妏傪兛偲偡傞乯
嘊倸幉乮倕l偲堦抳偟偰偄傞乯偱擟堄偺揰俼乮倶丆倷丆倸乯傪兤夞揮偝偣傞丅
嘋倶幉偱揰俼傪亅兛夞揮偝偣傞丅
嘍倸幉偱揰俼傪亅兞夞揮偝偣傞丅
倸幉偺廃傝偱夞揮偝偣偰傕丄倸幉偲倕l偺側偡妏偼曄傢傜側偄偺偱丄倸幉偲倕l偺側偡妏偼兛偱偁傞丅
傑偨丄倕l偺倶倷暯柺傊偺幩塭偑倷幉偲偺側偡妏偑兞偱偁傞偐傜丄兛偲兞傪梡偄傟偽丄
倢x亖倱倝値兛倱倝値兞
倢y亖倱倝値兛們倧倱兞
倢z亖們倧倱兛
偱梌偊傜傟傞丅
嘆倸幉廃傝偺夞揮側偺偱丄
乮倢x丄倢y丄倢z乯仺乮侽丆乮侾亅倢z2乯1/2丆倢z乯
傊曄姺偝傟傞丅
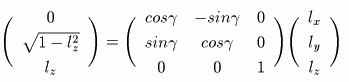
嘇倶幉廃傝偺夞揮側偺偱丄乮侽丆乮侾亅倢z2乯1/2丆倢z乯仺乮侽丆侽丆侾乯
傊曄姺偝傟傞丅
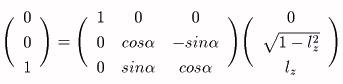
偙偙傑偱偺曄姺偵傛偭偰丄倕l偼倸幉偵堦抳偡傞丅摨條偺曄姺傪拲栚偡傞揰乮儀僋僩儖乯偵傕揔梡偡傟偽丄
揰俼乮倶丆倷丆倸乯偼丄嘆丄嘇偺曄姺偵傛偭偰
傑偲傔傟偽
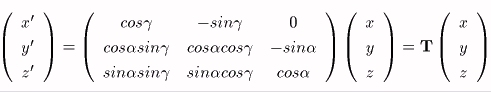
偱揰俼'乮倶'丆倷'丆倸'乯傊堏偝傟傞丅
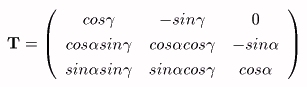
偙偙偱丄峴楍俿偼丄儀僋僩儖倕l傪乮侽丆侽丆侾乯傊堏偡曄姺偺堦偮乮曄姺嘆嘇乯傪昞偡丅
偙偺曄姺偱摼傜傟偨揰俼'傪倸幉偵娭偟偰兤夞揮偝偣偨揰俼''乮倶''丆倷''丆倸''乯偼師偺傛偆偵昞偝傟傞丅
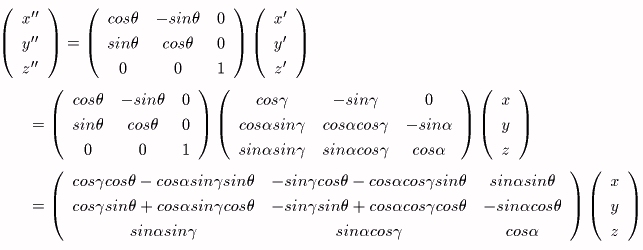
嘋丄嘍偺曄姺傕摨條偵峫偊偰峴偊偽丄倕l傪幉偲偟偨兤夞揮屻偺揰俼埵抲揰俼"乮倶'''丆倷'''丆倸'''乯偼師偺傛偆偵昞偝傟傞丅
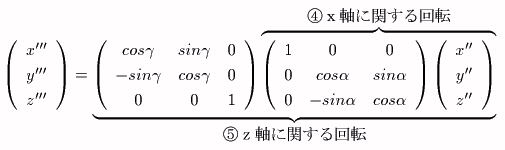
曄姺嘋嘍偑丄曄姺嘆嘇偺媡曄姺偱偁傞偙偲傪峫偊傞偲丄忋偺昞尰偼峴楍俿偺媡峴楍偵傛偭偰丄
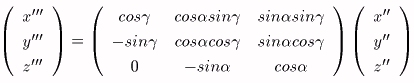
偲傕梌偊傜傟傞丅
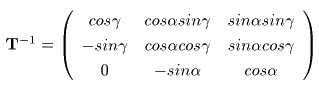
偲側偭偰偄傞偼偢偱偁傞丅
丂乮倶丆倷丆倸乯仺乮倶'''丆倷'''丆倸'''乯偺曄姺偼師偺傛偆偵昞偝傟傞丅
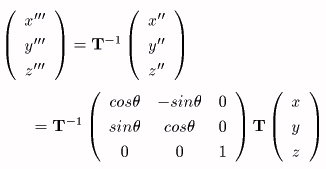
師偺峴楍倀偵傛偭偰丄倕l偺廃傝偺兤夞揮偑婰弎偝傟傞偙偲偑暘偐傞丅

偨偩偟丄兪亖侾亅們倧倱兤偲偍偄偨丅倢x丄倢y丄倢z偱偁傜傢偣偽丄
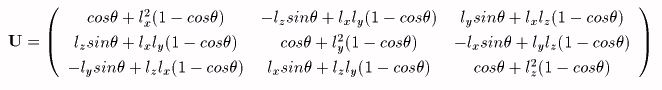
丂尨揰傪婲揰偲偡傞倕l乮亖乮倢x丄倢y丄倢z乯
丂乮扨埵儀僋僩儖偱偁傞偐傜丄倢x2亄倢y2亄倢z2亖侾乯傪幉偲偟偨兤夞揮乮倕l偺廔揰偐傜婲揰傪尒偨偲偒嵍夞傝偺夞揮傪惓偺曽岦偲偡傞乯偼丄夞揮慜偺揰傪倰丄夞揮屻偺揰傪倰'偲偡傟偽丄倰'亖倀倰偱梌偊傜傟傞丅傕偟丄倰偱壗偐偺宍傪梌偊傞揰偺廤崌偑戙昞偝傟偰偄傟偽丄倰'偺揰偺廤崌偱梌偊傜傟傞宍偼倰偺揰偺廤崌偺梌偊傞宍偲崌摨偲側傞丅乮揰傪倕l偵娭偟偰摨偠偩偗夞揮偡傞偺偱偁傞偐傜偁偨傝傑偊乯
丂椺偊偽丄乮侾丆侾丆侾乯幉傪拞怱偲偟偨2兾乛俁夞揮傪昞偡峴楍偼丄乮倢x丆倢y丆倢z乯亖乮侾乛俁1/2丆侾乛俁1/2丆侾乛俁1/2乯丄兤亖2兾乛俁偱偁傞偐傜丄
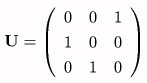
偱偁偨偊傜傟傞丅幚嵺丄偙偺曄姺傪峴偆偲倕x乮亖乮侾丆侽丆侽乯乯仺倕y乮亖乮侽丆侾丆侽乯乯丄倕y仺倕z乮亖乮侽丆侽丆侾乯乯丄倕z仺倕x偵側傞偙偲偑暘偐傞丅
偙傟偱偙偺崁栚偼廔傢傝
揹婥岺妛偱巊偆悢妛揑庤朄偺擖傝岥儁乕僕
儁乕僕偺慖戰
堜屗丒揷嫶亄屻摗丂尋媶幒僩僢僾儁乕僕