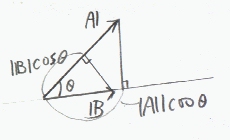
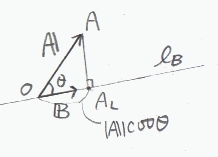
右の図において、ベクトルＡとＢを考える。ただし、Ａ、Ｂとも始点はＯにあるとする。
Ｂを含む直線ｌBを考えて、Ａの終点ＡからｌBにおろした垂線の足をＡLとする。
（線分ＯＡLはＡのB(ｌB)の方向の成分になっている。これは、ｌBをｘ軸だと思えば、
線分ＯＡLがＡのｘ成分になっている事と同じ事である。）
いま、線分の長さＯＡLは、ＡとｌBのなす角をθとすると
|Ａ|ｃｏｓθ
と書ける。
ここで、|Ａ|ｃｏｓθと|Ｂ|の積をＡとＢの内積と呼び、Ａ・Ｂと表現する。
Ｂが単位ベクトルｅBの場合には、Ａ・ｅB=|Ａ|ｃｏｓθであるから、
Ａ・ｅBは、ＡのｅB方向成分を表す。
(ＡのｅBへの射影の大きさをあらわす。）
Ａ・Ｂ=Ａ・|Ｂ|ｅB=Ａ・ｅB|Ｂ|
なので、内積Ａ・ＢはＡのＢ方向成分(ｅB方向成分)にＢの大きさを掛けた量を表すともいえる。
Ａ・Ｂについてもう少し考える。
Ａ・Ｂ=|Ａ|ｃｏｓθ|Ｂ|=|Ａ||Ｂ|ｃｏｓθ
|Ａ|ｃｏｓθ は、ＡのＢ方向成分を表すので、Ａ・Ｂは、
ＡのＢ方向成分にＢの大きさを掛けた大きさを表すといえる。
また、|Ｂ|ｃｏｓθ は、ＢのＡ方向成分を表すので、Ａ・Ｂは、
ＢのＡ方向成分にＡの大きさを掛けた大きさを表すともいえる。
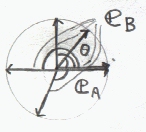
Ａの単位ベクトルをｅA、 Ｂの単位ベクトルをｅBとすると
Ａ・Ｂ=|Ａ|ｅA・|Ｂ|ｅB =|Ａ||Ｂ|ｅA・ｅB
ここで、ｅA・ｅBは、ｅA・ｅB=ｃｏｓθ θはｅAとｅBの成す角（ＡとＢの成す角）となる。
この値は、たとえば
ｅAとｅBが同じ向きで平行の時 '1'
ｅAとｅBが逆向きで平行の時 '-1'
ｅAとｅBが垂直の時 '0'
ｅAとｅBの成す角が鋭角なら'1〜0'
ｅAとｅBの成す角が鈍角なら'0〜-1'
となり、二つのベクトルの平行の度合の様なものを表すともいえる。
Ａ・Ｂは、Ａの大きさとＢの大きさの積に、平行の度合を掛けたものともいえる。
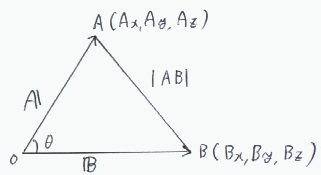内積をベクトルの成分で表すことを考える。右図のように、原点Ｏを始点とする位置ベクトルＡ、Ｂ
を考える。
（Ａ＝（Ａx,Ａy,Ａz）、Ｂ＝（Ｂx,Ｂy,Ｂz））
三角形ＯＡＢで、ＯＡとＯＢのなす角をθとして余弦定理を使えば、
|ＡＢ|2＝|Ａ|2＋|Ｂ|2−２|Ａ||Ｂ|cosθ
|ＡＢ|2＝（Ａx−Ｂx）2＋（Ａy−Ｂy）2＋（Ａz−Ｂz）2
＝|Ａ|2＋|Ｂ|2−２（ＡxＢx＋ＡyＢy＋ＡzＢz）
これを上の式に代入して両辺を入れ替えれば、
−２|Ａ||Ｂ|cosθ＝−２（ＡxＢx＋ＡyＢy＋ＡzＢz）
|Ａ||Ｂ|cosθ＝ＡxＢx＋ＡyＢy＋ＡzＢz
＝Ａ・Ｂ
Ａ・Ｂ＝|Ａ||Ｂ|cosθ＝ＡxＢx＋ＡyＢy＋ＡzＢz
と表現される。（成分毎の積の和で与えられる。）
Ａ・Ｂ＝ＡxＢx＋ＡyＢy＋ＡzＢz
Ｂ・Ａ＝ＢxＡx＋ＢyＡy＋ＢzＡz＝
Ａ・Ｂ
よって、交換則が成り立つ。
Ｃ＝（Ｃx,Ｃy,Ｃz）とすれば、
Ａ±Ｃ＝（Ａx±Ｃx,Ａy±Ｃy,Ａz±Ｃz）より、
（Ａ±Ｃ）・Ｂ＝（Ａx±Ｃx）Ｂx＋（Ａy±Ｃy）Ｂy
＋（Ａz±Ｃz）Ｂz
＝ＡxＢx±ＣxＢx＋ＡyＢy±ＣyＢy
＋ＡzＢz±ＣzＢz
＝（ＡxＢx＋ＡyＢy＋ＡzＢz）±（ＣxＢx＋ＣyＢy＋ＣzＢz）
＝Ａ・Ｂ±Ｃ・Ｂ
よって、分配則が成り立つ。
まとめれば、
Ａ・Ｂ＝Ｂ・Ａ
（Ａ±Ｃ）・Ｂ＝Ａ・Ｂ±Ｃ・Ｂ