丂
丂埵抲倰乮亖乮倶丆倷丆倸乯乯傪曄悢偵偡傞娭悢偱奺惉暘偑昞偝傟傞儀僋僩儖俥(=乮俥x乮倰乯,俥y乮倰乯,俥z乮倰乯乯傪峫偊傞丅
丂儀僋僩儖俥偵懳偟偰丄偦傟偧傟偺曽岦惉暘傪懳墳偡傞曄悢偱曃旝暘偟偨検偺榓
丂丂佪俥x/佪倶+佪俥y/佪倷+佪俥z/佪倸
傪儀僋僩儖俥偺敪嶶(divergence)偲屇傃丄div俥偲昞偡丅 旝暘墘嶼巕佫傪巊偭偰偁傜傢偣偽丄敪嶶偼丄佫偲俥偺撪愊偱丄佫丒俥丂偲昞偣傞丅
XYZ嵗昗偵偍偄偰偼丄div俥(=佫丒俥)=佪俥x/佪倶+佪俥y/佪倷+佪俥z/佪倸
偲昞偝傟傞偑丄懠偺嵗昗宯偱偼佫偺昞尰偑堎側傞偺偱丄堎側傞昞尰偵側傞丅
丂丂div俥偺堄枴偵偮偄偰峫偊傞丅
丂嬻娫偵枾搙兿乮倰丆倲乯偱'壗偐'乮椺偊偽丄偨偽偙偺墝偺棻巕乯偑暘晍偟偰偄傞偲偡傞丅乮兿偼埵抲偲帪娫偺曄悢偱梌偊傜傟傞丅乯
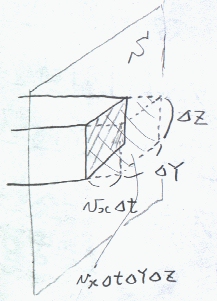
丂偙偙偱丄帪崗倲偐傜倲亄嚈倲偵偍偄偰揰倰偺嚈倶嚈倷嚈倸偱埻傑傟傞旝彫椞堟撪偱偺棻巕悢偺曄壔嚈兿傪峫偊傞丅
崱丄偨偽偙偺墝偺儅僋儘側摦偒乮'備傜備傜偲昚偭偰偄傞墝偺摦偒'傗'晽偵悂偐傟偰備偔墝偺摦偒'乯偺懍搙傪
倴乮亖(倴x,倴y,倴z)乯
偲偡傞丅柺俽偵奐偄偨嚈倄嚈倅偺柺傪嚈倲帪娫偺娫偵塃偐傜嵍傊敳偗傞棻巕偺悢値x偼丄捠傝敳偗傞懱愊偑丄倴x嚈倲嚈倄嚈倅偱偁傞偐傜丄棻巕偺枾搙傪兿偲偡傟偽丄
値x亖兿倴x嚈倲嚈倷嚈倸
偱梌偊傜傟傞丅崱丄兿倴x偼倶曽岦偺扨埵抐柺愊傪扨埵帪娫摉傝偵乮倶曽岦偵乯棳傟傞棻巕偺検乮棻巕棳枾搙乯傪昞偡丅倷丆倸曽岦偵傕棻巕棳偼偁傞偺偱丄偦傟偧傟偺曽岦偺棻巕棳枾搙傪惉暘傪偲偡傞棻巕棳枾搙偺儀僋僩儖
倞乮亖(倞x,倞y,倞z)亖兿倴亖(兿倴x,兿倴y,兿倴z)乯
偱値x傪偁傜傢偣偽丄値x亖倞x嚈倲嚈倷嚈倸偲偐偗傞丅
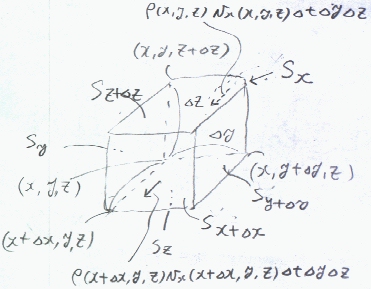
丂偝偰丄揰倰偵旝彫側嚈倶嚈倷嚈倸側傞戝偒偝偺捈曽懱傪峫偊傞丅偁傞帪娫倲偵偍偗傞偙偺捈曽懱撪晹偺棻巕悢傪嚈俶乮倶丆倷丆倸丆倲乯偲偟丄
嚈倲帪娫屻偺棻巕悢嚈俶乮倶丆倷丆倸丆倲亄嚈倲乯傪媮傔傞丅捈曽懱傪峔惉偡傞偦傟偧傟偺柺
俽x,俽x+嚈x,俽y,俽y+嚈y,俽z,俽z+嚈z
傪捠夁偡傞棻巕偺悢傪偨偣偽丄捈曽懱撪偺棻巕悢偑摼傜傟傞丅俽x傪棻巕偑捠夁偡傞偲棻巕悢偑憹壛偟乮捈曽懱偵擖傞曽岦乯丄俽x+嚈x傪棻巕偑捠夁偡傞偲棻巕悢偑尭彮偡傞偺偱丄乮捈曽懱偐傜弌傞曽岦乯倶曽岦偺棳傟偵傛傞棻巕偺憹壛偼丄
倞x乮倶丆倷丆倸乯嚈倲嚈倷嚈倸亅倞x乮倶+嚈倶丆倷丆倸乯嚈倲嚈倷嚈倸偲側傞丅
倞x乮倶+嚈倶丆倷丆倸乯傪嚈倶偵偮偄偰揥奐偟偰堦師傑偱傪峫偊傟偽丄
倞x乮倶丆倷丆倸乯嚈倲嚈倷嚈倸+佪倞x乮倶丆倷丆倸乯/佪倶*嚈倶嚈倲嚈倷嚈倸
偲側傞丅倶曽岦偺棳傟偵傛傞棻巕偺憹壛偼丄
倞x乮倶丆倷丆倸乯嚈倲嚈倷嚈倸亅倞x乮倶+嚈倶丆倷丆倸乯嚈倲嚈倷嚈倸亖亅佪倞x乮倶丆倷丆倸乯/佪倶*嚈倶嚈倲嚈倷嚈倸
倷丆倸曽岦偵偮偄偰傕摨條偵峫偊偰偡傋偰偨偣偽丄捈曽懱偵擖傞棻巕偺憤榓偑摼傜傟傞丅偙傟偼丄師偺幃偱梌偊傜傟傞丅
亅佪倞x乮倶丆倷丆倸乯/佪倶*嚈倶嚈倲嚈倷嚈倸亅佪倞y乮倶丆倷丆倸乯/佪倷*嚈倷嚈倲嚈倸嚈倶亅佪倞z乮倶丆倷丆倸乯/佪倸*嚈倸嚈倲嚈倶嚈倷
=亅(佪倞x乮倶丆倷丆倸乯/佪倶+佪倞y乮倶丆倷丆倸乯/佪倷+佪倞z乮倶丆倷丆倸乯/佪倸)*嚈倲嚈倶嚈倷嚈倸
=-div倞嚈倲嚈倶嚈倷嚈倸(=-佫丒倞*嚈倲嚈倶嚈倷嚈倸)
捈曽懱撪晹偵擖偭偰備偔棻巕偺悢偑晧偺敪嶶偱梌偊傜傟傞偙偲偐傜丄棻巕棳枾搙偺敪嶶偼丄乮扨埵懱愊摉傝偺乯奜傊弌偰偄偔棻巕偺検傪梌偊傞偙偲偑暘偐傞丅
捈曽懱偵擖傞棻巕偺憤榓偼丄嚈俶乮倶丆倷丆倸丆倲亄嚈倲乯-嚈俶乮倶丆倷丆倸丆倲乯偱傕梌偊傜傟傞偺偱丄
嚈俶乮倶丆倷丆倸丆倲亄嚈倲乯-嚈俶乮倶丆倷丆倸丆倲乯亖-佫丒倞嚈倲嚈倶嚈倷嚈倸
嚈俶乮倶丆倷丆倸丆倲亄嚈倲乯/嚈倶嚈倷嚈倸-嚈俶乮倶丆倷丆倸丆倲乯/嚈倶嚈倷嚈倸亖-佫丒倞嚈倲
嚈俶乮倶丆倷丆倸丆倲乯/嚈倶嚈倷嚈倸偼懱愊撪偺棻巕悢傪懱愊偱妱傞偺偱枾搙兿偵摍偟偄丅備偊偵丄
兿乮倶丆倷丆倸丆倲亄嚈倲乯-兿乮倶丆倷丆倸丆倲乯亖-佫丒倞嚈倲
兿乮倶丆倷丆倸丆倲亄嚈倲乯傪嚈倲偺堦師傑偱揥奐偡傟偽丄兿乮倶丆倷丆倸丆倲乯+佪兿乮倶丆倷丆倸丆倲乯/佪倲*嚈倲側偺偱丄
兿乮倶丆倷丆倸丆倲亄嚈倲乯-兿乮倶丆倷丆倸丆倲乯亖佪兿乮倶丆倷丆倸丆倲乯/佪倲*嚈倲亖-佫丒倞嚈倲
丂丂佪兿乮倶丆倷丆倸丆倲乯/佪倲亖-佫丒倞乮倶丆倷丆倸丆倲乯
丂丂佫丒倞+佪兿/佪倲亖侽丂(倞亖兿倴)
丂偙傟偼丄偁傞揰偵偍偄偰乮扨埵懱愊摉偨傝偺乯棻巕偺惗惉徚柵偑柍偄応崌偺棻巕偺憹尭偲棻巕偺棳傟偺娭學乮棻巕悢偑晄曄偱偁傞偙偲乯傪昞偡丅楢懕偺幃偲偄偆丅乮倞傪揹棳枾搙丄兿傪揹壸枾搙偲偡傟偽丄揹壸曐懚懃傪偁傜傢偡丅乯
丂傕偟丄旝彫捈曽懱撪偵壩偺偮偄偨偨偽偙偑偁傟偽丄捈曽懱偵擖傞棻巕偼側偔偰傕丄棻巕悢偼憹壛偡傞丅 傑偨丄旝彫捈曽懱撪偵棻巕偺媧拝嵻偑偁傟偽丄弌偰偄偔棻巕偼側偔偰傕棻巕悢偼尭彮偡傞丅偙傟傜偺検偼丄偦偺応強偱偺棻巕偺惗惉徚柵偵憡摉偡傞丅 扨埵帪娫扨埵懱愊摉傝偺惗惉傪倗丄徚柵傪倱偲偡傟偽丄
丂丂佫丒倞+佪兿/佪倲亖倗-倱
偱梌偊傜傟傞丅
揰倰乮亖倶丆倷丆倸乯乯偵偍偗傞儀僋僩儖倞偺曽岦偵倶幉傪偲傞丅 揰倰偺嬤朤偱丄倞偺曽岦偑曄傢傜側偗傟偽丄
倞乮倰乯亖乮倞x丆侽丆侽乯丄倞乮倰亄嚈倰乯亖乮倞x乮倰亄嚈倰乯丆侽丆侽乯
偲倃幉惉暘偟偐懚嵼偟側偄丅偙偺偲偒div倞=佪倞x/佪倶偲偐偗傞丅 偙傟偼丄偁傞揰乮偙偙偱偼倰乯偺嬤朤偱儀僋僩儖乮偙偙偱偼倞乯偺曽岦偑曄傢傜側偄帪丄 敪嶶偑丄'偦偺儀僋僩儖偺曽岦傊堏摦偟偨偲偒偺儀僋僩儖偺戝偒偝偺曄壔棪傪偁傜傢偡'偙偲傪帵偡丅
曄壔棪偵嬻娫偱偺堏摦検乮倞偺曽岦傊偺堏摦検乯傪偐偗傟偽丄儀僋僩儖偺戝偒偝偺曄壔検偑摼傜傟傞丅 倞偺曽岦偵倶幉傪慖傋偽丄
嚈倞x亖佪倞x/佪倶嚈倶亖div倞嚈倶