スカラをスカラで積分する

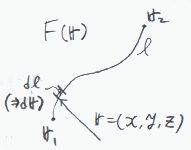
三次元空間で定義される関数F(r)を点r1からr2まで経路Lにしたがって距離によって積分する表現を考える。
経路を線と考えれば、一つの変数(ここでは、't'とする)で線は表現される。つまり、経路の線上の点r(=x(t),y(t),z(t))の各成分は、ただ一つの’媒介変数’tの関数で表現される。(もちろんx(yやz)を媒介変数として使ってもよい)
さて、線の大きさだけに対する積分の一般表現は、∫F(r)d l(d l;Lに沿って積分する)である。
点r(=(x(t),y(t),z(t)))の集合が、線Lをあらわせば、d lと|d r|は等しくなる。
今、媒介変数によってd lとd rを関連づける。
d lは、線L上での点rからr+d r迄の長さ|d r|である。
d l=|d r|=|(d x,d y,d z)|=(d x2+d y2+d z2)1/2
媒介変数tでそれぞれの変位をあらわすとd x=d x/d t*d t、・・とかける。d tでくくり出せば、d t>0(tを増やす方向に積分)として、
d l=((d x/d t)2+(d y/d t)2+(d z/d t)2)1/2d t
よって次のように与えられる。
∫F(r)d l=∫F(x(t),y(t),z(t))((d x/d t)2+(d y/d t)2+(d z/d t)2)1/2d t
面積分と体積積分で扱ったようにrを一つの独立変数tによる表現で表せば、(rの集合は線を表すので、点rの集合を記述する独立変数は一つ)
∫Fd l=∫F(t)|d r/d t|d t
rを成分で表せば、先ほどの式になる。
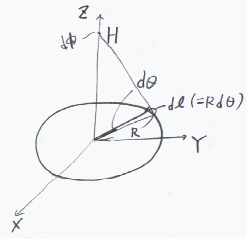
例えば、太さを無視できる半径Rの円環状に線電荷密度λ〔C/m〕で電荷が分布する時、円環の中心軸上の円環からの距離H (円環の中心軸をz軸とし、円環を含む平面をz=0とする)の位置での電位φを求める。
電荷の分布は、XYの座標軸を設定して、媒介変数θを使って、(X,Y,Z)=(Rcosθ,Rsinθ,0)で与えられる。(θは、XY面内でX軸からのなす角に相当する。)
円環の経路は、θ;0〜2π で表される。
円環上の微小線分dlによるHでの電位dφは、距離が(H2+X2+Y2)1/2であるから
X2+Y2=R2であるから
dφ=λdl/4πε0(H2+R2)1/2
dl=((dX/dt)2+(dY/dt)2+(dZ/dt)2)1/2dt=((-Rsinθ)2+(Rcosθ)2)1/2dθ=Rdθ であるから、(dl=Rdθになるのは、作図をみれば明らか)
φ=∫dφ=∫λdl/4πε0(H2+R2)1/2(dl;円環に沿った経路)=∫λ/4πε0(H2+R2)1/2Rdθ(θ;0〜2π)
=λ/4πε0(H2+R2)1/2*2πR
=λR/2ε0(H2+R2)1/2
ベクトルをスカラで積分する
例えば、'太さを無視できる半径Rの円環上に均一に線電荷蜜度λ(C/m)で電荷が分布する場合、円環の中心軸上の円環からの距離H (円環の中心軸をz軸とし、円環を含む平面をz=0とする)の位置での電界Eを求める。'で示したように、各成分それぞれの線積分を求めれば良い。
ベクトルをベクトルで内積を取りながら積分する
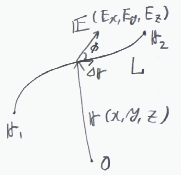
三次元空間で定義されるベクトル関数E(r)を点r1からr2まで経路Lにしたがって Lの接線方向(drのこと。rがL上を移動する時変化drはLの接線の方向をあらわす)との内積を取りながら距離に対して積分する(Eの'rの移動方向'の成分を移動距離に対して積分する)表現を考える。
さて、積分の一般表現は、∫E・dr(;Lに沿って積分する)である。
∫E・drにおいて、E・dr=EXdX+EYdY+EZdZと分解されるので、
各項について一つの独立変数で積分を表現して、(第一項でXをそのまま積分変数とすれば、yとzは、xで表される従属変数)各項を別々に積分して値を求めることができる。
(すべての項を共通の独立変数で表しても良い。スカラのスカラによる積分と同じになる。)
(積分経路によって、ある変数について多価関数になるときには、値の重なりを考慮して積分する必要がある。
重なった領域においては、それぞれの領域に分けて積分する。)
またEとdrのなす角をφとすれば、E・dr=|E||dr|cosφであるから、 スカラ関数|E|cosφをスカラ|dr|で積分することになる。(もちろん、スカラ関数の変数は'積分変数(一つの変数)だけで'表現されねばならない)
もし、ベクトル関数E(r)がスカラ関数U(r)によって
E(r)=gradU(r)と表されれば、gradU(r)・dr=dUであるから
∫E・dr(dr;r1〜r2)
=∫gradU(r)・dr(dr;r1〜r2)
=∫dU(dU;r1〜r2)=U(r2)-U(r1)
とかける。この積分は、二点間のUの差で与えられることから、経路Lによらず一定であることが分かる。