① 円筒導体2の外側表面を接地して、円柱導体1に単位長さ当たりλ[C/m]の電荷を与えた。円筒導体2に分布する電荷を求めよ。
円筒導体2について---
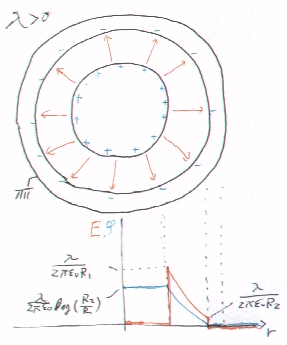
導体では、電荷は表面に分布し、導体内部には電界は存在しない。円筒導体の内側表面のごく内側での電界が、λ/2πε0R2であることを考慮して、円筒導体の内側表面を挟んでガウスの定理を用いれば、円筒導体の内側表面には、-λ/2πR2[C/m2]の電荷が分布することが導かれる。円筒導体の外側表面は、接地されており、電位は'0'である。無限の遠方でも電位は'0'であるから、円筒導体の外側表面には電荷は分布しない。
② ①において、円柱導体1の中心軸からの距離r[m]における電界の大きさを求めよ。
③ ①において、円柱導体1の中心軸からの距離R[m]における電位を求めよ。
④ ③において、全体を比誘電率εrの媒質で満たした。電位はどうなるか。
⑤ ④において、円柱導体1と円筒導体2の間の単位長さ当たりの静電容量を求めよ。
⑥ εr=3、R1=2.2[mm]、R2=6[mm]、t=0.1[mm]とする。
⑤において、単位長さ当たりの静電容量はいくらか。 ( ただし、loge(3/1.1)=1、ε0=8.854×10-12[F/m]として計算してもよい。)
II 比誘電率εrで厚さT[m]の無限に広い誘電体板を電界E[V/m]の一様電界中においた。ただし、誘電体板の表面が電界の方向と垂直になるようにおいた。次の問に答えよ。
① 誘電体板内部の電束密度を求めよ。
② 誘電体内部の電界を求めよ。
③ 誘電体表面に誘起される電荷の面密度を求めよ。
III 真空中の点(1,1,0)[m]にQ1[C]の点電荷、点(-1,-1,0)[m]にQ2[C]の点電荷がある。 以下の問いに答えよ。
① Q1=-Q2=1×10-9[C]のとき、
原点における電界、電位、電束密度、単位体積当たりの静電エネルギーを求めよ。
電位は、それぞれの点電荷による電位を足せばよい。両方の点電荷から等距離にあるので、0〔V〕
電束密度はε0E=7.97×10-11(-1,-1,0)/21/2〔C/m2〕
単位体積当たりの静電エネルギーはE・D/2であるので、3.58×10-10〔J/m3〕
② ①で、全体を比誘電率 2 の媒質で満たした。原点における電界、電位、電束密度を求めよ。
電位は、もともと0〔V〕であるから、0〔V〕
電束密度は変わらず、7.97×10-11(-1,-1,0)/21/2〔C/m2〕
③ ①で、電位が0[V]の等電位面を求めよ。
④ ②で、1[C]の点電荷を、x軸上の正の無限の遠方から原点まで移動させた。この点電荷の得たポテンシャルエネルギーを求めよ。