傕偟丄兟乮X亅X侽乯偲昞偣偽丄兟乮侽乯偼丄X亖X侽偺帪偵丄乫侽乫偱側偄抣傪帩偮丅乮愊暘抣偼傕偪傠傫乫侾乫乯 乮崟偄慄乮僌儔僼乯傪嶲徠乯
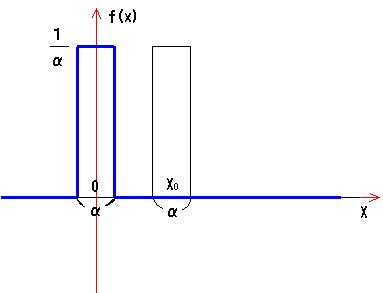
 塃偺恾偵偍偄偰丄埲壓偺嘆媦傃嘇偺忦審傪枮偨偡偲偒丄倖乮X乯傪僨儖僞娭悢偲偄偄兟乮X乯偱昞偡丅
塃偺恾偵偍偄偰丄埲壓偺嘆媦傃嘇偺忦審傪枮偨偡偲偒丄倖乮X乯傪僨儖僞娭悢偲偄偄兟乮X乯偱昞偡丅
嘆丂倖乮X乯偼丄X亗侽偺帪丄倖乮X乯亖侽偱丄X亖侽偺帪丄倖乮X乯亗侽偱偁傞丅
嘇丂 X乮愊暘斖埻偵X亖侽傪娷傓乯亖侾
偡側傢偪丄兟娭悢偲偼丄X亖侽偵偺傒乫侽乫偱側偄抣偑偁傝乮偦偺懠偺応強偱偼抣偼乫侽乫乯丄X幉偲埻傑傟偨椞堟偺柺愊偑侾偵側傞娭悢偺偙偲偱偁傞丅
乮惵偄慄乮僌儔僼乯傪嶲徠乯
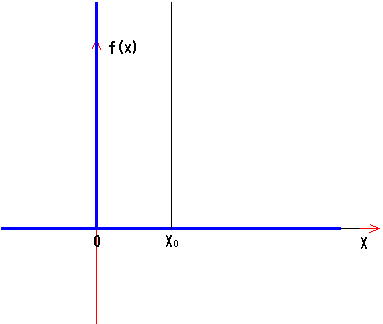
傕偟丄兟乮X亅X侽乯偲昞偣偽丄兟乮侽乯偼丄X亖X侽偺帪偵丄乫侽乫偱側偄抣傪帩偮丅乮愊暘抣偼傕偪傠傫乫侾乫乯
乮崟偄慄乮僌儔僼乯傪嶲徠乯

椺偊偽丄塃偺恾偵偍偄偰兛偑偳傫側抣偱偁傠偆偲X幉偲埻傑傟偨椞堟偺柺愊乮愊暘抣乯偼乫侾乫偱偁傞丅
兛偑桳尷偺帪偵偼丄亅兛乛俀亙X亙兛乛俀偱丄倖乮X乯亗侽偱偁傞偑丄兛仺侽偺応崌偵偼丄X亖侽偱偺傒抣偑乫侽乫偱側偔側傞偺偱兟乮X乯娭悢偲側傞丅乮偙偺偲偒倖乮X乯仺亣偱偁傞丅乯
値師尦偱偁傟偽丄値師尦偺兟娭悢偑掕媊偝傟傞丅値師尦偺曄悢傪儀僋僩儖倰偱昞偣偽丄兟乮倰亅倰侽乯偼丄
倰亗倰侽偱丄乫侽乫偲側傝丄
| 佺 | 兟乮倰亅倰侽乯d V乮値師尦偺懱愊愊暘乯丂亖丂 | { | 丂侾丂丗丂愊暘斖埻偵倰侽傪娷傓乯 丂侽丂丗丂愊暘斖埻偵倰侽傪娷傑側偄乯 |
偙偺娭悢偵偼丄桳梡側懡偔偺惈幙偑偁傞丅堦師尦乮庡偵帪娫曄悢乯偺応崌偲嶰師尦乮庡偵埵抲曄悢乯偺応崌偵偮偄偰夝愢偡傞丅