倂亖佺倁d俻亖俠倁2/俀亖俻2/俀俠亖俻倁/俀
偲昞偝傟傞丅 埲壓偵婔偮偐偺椺傪弎傋傞丅

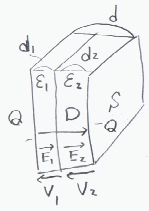
斾桿揹棪偺堎側傞桿揹懱傪廳偹偰椉懁偵揹嬌傪偮偗偨峔憿傪峫偊傞丅
嬌斅偺柺愊傪俽嬌斅偺娫妘傪倓丄桿揹懱偼丄桿揹棪兠1丄岤偝倓1丄桿揹棪兠2丄岤偝倓2乮倓亖倓1亄倓2乯偱偁傞偲偡傞丅
僐儞僨儞僒偺崁栚傪嶲峫偵偡傞偲丄惷揹梕検俠偼丄
侾/俠亖乮倓1/兠1亄倓2/兠2乯/俽
偱偁傞丅
揹壸検傪俻偱堦掕偵曐偭偨偲偒偺惷揹僄僱儖僊乕倂偲椡傪媮傔傞丅
倂亖俻2/俀俠亖俻2/俀俽*乮倓1/兠1亄倓2/兠2乯
丂亖俻2/俀俽*乮倓1/兠1亄乮倓亅倓1乯/兠2乯
椡俥偼俥亖亅佪倂/佪倓1偱偁傞偐傜丄
俥亖俻2/俀俽*乮侾/兠2亅侾/兠1乯
偲側傞丅扨埵柺愊摉傝偺椡倖乮亖俥/俽乯偼丄
倖亖侾乛俀乮俻/俽乯2乮侾/兠2亅侾/兠1乯
揹壸検偑堦掕偱偁傞偐傜丄惷揹僄僱儖僊乕偺尭彮偼丄揹埑偺掅壓偵傛傞丅揹埑偺掅壓偼丄桿揹棪偺憹壛偵傛偭偰婲傞偺偱丄桿揹棪偺彫偝偄
兠1偺攠幙偑丄弅傕偆偲偡傞丅
偙偙偱丄桿揹棪兠1偺攠幙撪偺揹奅俤1偼丄揹懇枾搙俢偑丄
俢亖俻/俽偱偁傞偐傜丄俢亖兠1俤1亖兠2俤2傪峫椂偟偰丄
椡倖傪彂偒姺偊傞偲乮崱偺応崌偼丄俢1亖俢2亖俢偱偁傞偑乯
倖亖亅俢12/俀兠1亄俢22/俀兠2
丂亖亅俤1俢1/俀亄俤2俢2/俀
揹埑傪倁偱堦掕偵曐偭偨偲偒偺惷揹僄僱儖僊乕倂偲椡傪媮傔傞丅
倂亖俠倁2/俀亖俽倁2/俀乮倓1/兠1亄倓2/兠2乯
丂亖俽倁2/俀乮倓1/兠1亄乮倓亅倓1乯/兠2乯
娫妘傪倓1仺倓1亄嚈倓1傊曄壔偝偣偨偲偒偺僐儞僨儞僒偺僄僱儖僊乕偺曄壔偼丄
丂佪倂/佪倓1丒嚈倓1
偲側傞丅偙偺偲偒摨帪偵丄揹壸検偑嚈俻乲俠乴憹壛偡傞丅偙偺揹壸偼丄揹埑倁乲倁乴偺揹尮傛傝嫙媼偝傟偰偄傞偺偱丄揹尮偱嚈俻倁乲俰乴偺僄僱儖僊乕偺尭彮偑婲偙傞丅 慡懱偲偟偰丄憹壛偟偨僄僱儖僊乕嚈倂net偼丄嚈倂net亖佪倂/佪倓1丒嚈倓1亅嚈俻倁
椡俥偼俥亖亅佪倂net/佪倓1偱偁傞偐傜丄
俥亖亅俽倁2/俀乮倓1/兠1亄乮倓亅倓1乯/兠2乯2*乮侾/兠1亅侾/兠2乯
偲側傞丅扨埵柺愊摉傝偺椡倖乮亖俥/俽乯偼丄
倖亖亅倁2/俀乮倓1/兠1亄倓2/兠2乯2*乮侾/兠1亅侾/兠2乯
揹埑偑堦掕偱偁傞偐傜丄惷揹僄僱儖僊乕偺尭彮偼丄揹壸偺尭彮偵傛傞丅揹壸偺尭彮偼丄桿揹棪偺掅壓偵傛偭偰婲傞偺偱丄桿揹棪偺彫偝偄
兠2偺攠幙偑丄挴傜傕偆偲偡傞丅
偙偙偱丄桿揹棪兠1偺攠幙撪偺揹奅俤1偼丄揹懇枾搙俢偑丄
俢亖俻/俽亖俠倁/俽亖倁/乮倓1/兠1亄倓2/兠2乯
偱偁傞偐傜
俤1亖俢/兠1亖倁/乮倓1/兠1亄倓2/兠2乯兠1
摨條偵丄桿揹棪兠2撪偺揹奅俤2偼丄
俤2亖俢/兠2亖倁/乮倓1/兠1亄倓2/兠2乯兠2
偙傟傜傪巊偭偰丄椡倖傪彂偒姺偊傞偲乮崱偺応崌偼丄俢1亖俢2亖俢偱偁傞偑乯
倖亖兠2俤22/俀亅兠1俤12/俀
丂亖俤2俢2/俀亅俤1俢1/俀
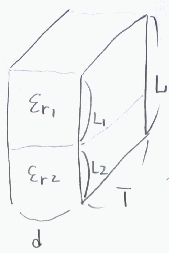
兠r1丄兠r2偺攠幙偺椉抂偺揹嬌偼揹埵偑摍偟偄丅傛偭偰丄揹奅俤偼椉攠幙撪偱摍偟偄丅
兠r1偺攠幙撪偺揹懇枾搙俢1偼丄兠0兠r1俤偲側傞丅
摨條偵兠r2偺攠幙撪偺揹懇枾搙俢2偼丄兠0兠r2俤偲側傞丅
揹懇枾搙偼丄揹嬌偺柺揹壸枾搙偵摍偟偄偺偱丄兠r1偺攠幙偺椉抂偺揹壸検俻1偼丄兠0兠r1俤俴1俿偲側傞丅
摨條偵丄兠r2偺攠幙偺椉抂偺揹壸検俻2偼丄兠0兠r2俤俴2俿偲側傞丅
慡揹壸検偼丄俻乮們乯偱偁傞偐傜丄俻亖俻1亄俻2
俻亖兠0兠r1俤俴1俿亄兠0兠r2俤俴2俿
丂亖兠0俿乮兠r1俴1亄兠r2俴2乯俤
揹埑倁偼俤倓傛傝丄
倁亖俻倓/兠0俿乮兠r1俴1亄兠r2俴2乯
慡僄僱儖僊乕倂偼丄倂亖俻倁/俀偱梌偊傜傟傞丅
倂亖俻2倓/俀兠0俿乮兠r1俴1亄兠r2俴2乯
丂亖俻2倓/俀兠0俿乮兠r1俴1亄兠r2乮俴亅俴1乯乯
俥亖亅佪倂/佪俴1亖俻2倓/俀兠0俿乮兠r1俴1亄兠r2俴2乯2*乮兠r1亅兠r2乯
椡偺戝偒偝偼丄俻2倓/俀兠0俿乮兠r1俴1亄兠r2俴2乯2*乮兠r1亅兠r2乯偱偁傞丅
兠r1亜兠r2偺帪丄俴1偑挿偔側傞曽岦傊摥偔丅
扨埵柺愊摉傝偺椡倖乮亖俥/倓俿乯傪媮傔傞偲
倖亖俻2倓/俀兠0俿2倓乮兠r1俴1亄兠r2俴2乯2*乮兠r1亅兠r2乯
丂亖兠0乮兠r1亅兠r2乯俤2/俀乮俤偼攠幙撪偺揹奅乯
丂亖俢1俤/俀亅俢2俤/俀乮俤乮亖俤1亖俤2乯偼攠幙撪偺揹奅丄俢偼偦傟偧傟偺攠幙偺揹懇枾搙乯
丂亖俢1俤1/俀亅俢2俤2/俀
揹埑堦掕偺帪偲斾妑偟偰丄椡偺戝偒偝偼摨偠偱丄岦偒偑媡岦偒偱偁傞偙偲偑暘偐傞丅
仈揹壸検偑堦掕偱偁傞偐傜丄僄僱儖僊乕偑尭彮偡傞偺偼丄揹埵偑彫偝偔側傞帪偱偁傞丅
桿揹棪偑戝偒偔側傞傎偳揹埵偼彫偝偔側傞偺偱丄桿揹棪偺戝偒偄椞堟偑戝偒偔側傠偆偲偡傞椡偑摥偔丅
嘇僐儞僨儞僒偵堦掕偺揹埑倁乮倁乯傪報壛偟偨帪丄惷揹僄僱儖僊乕偲桿揹懱偺嫬奅偵敪惗偡傞椡傪媮傔傞丅
兠r1丄兠r2偺攠幙偺椉抂偺揹嬌偼揹埵偑摍偟偄丅傛偭偰丄揹奅偼倁/倓偱椉攠幙撪偱摍偟偄丅
兠r1偺攠幙撪偺揹懇枾搙俢1偼丄兠0兠r1倁/倓偲側傞丅
揹懇枾搙偼丄揹嬌偺柺揹壸枾搙偵摍偟偄偺偱丄兠r1偺攠幙偺椉抂偺揹壸検俻1偼丄兠0兠r1倁/倓*俴1俿偲側傞丅
兠r2偺攠幙撪偺揹懇枾搙俢2偼丄兠0兠r2倁/倓偲側傞丅
揹懇枾搙偼丄揹嬌偺柺揹壸枾搙偵摍偟偄偺偱丄兠r2偺攠幙偺椉抂偺揹壸検俻2偼丄兠0兠r2倁/倓*俴2俿偲側傞丅
僐儞僨儞僒偱偺慡僄僱儖僊乕倂偼丄倂亖俻1倁/俀亄俻2倁/俀偱梌偊傜傟傞丅
倂亖兠0兠r1倁2/俀倓*俴1俿亄兠0兠r2倁2/俀倓*俴2俿
丂亖兠0倁2/俀倓*俿乮兠r1俴1亄兠r2俴2乯
丂亖兠0倁2/俀倓*俿乮兠r1俴1亄兠r2乮俴亅俴1乯乯
偲側傞丅偙偺偲偒摨帪偵丄揹壸検偑嚈俻乲俠乴憹壛偡傞丅偙偺揹壸偼丄揹埑倁乲倁乴偺揹尮傛傝嫙媼偝傟偰偄傞偺偱丄揹尮偱嚈俻倁乲俰乴偺僄僱儖僊乕偺尭彮偑婲偙傞丅 慡懱偲偟偰丄憹壛偟偨僄僱儖僊乕嚈倂net偼丄嚈倂net亖佪倂/佪俴1丒嚈俴1亅嚈俻倁
椡俥偼俥亖亅佪倂net/佪俴1偱偁傞偐傜丄
俥亖亅佪倂net/佪俴1亖兠0倁2/俀倓*俿乮兠r1俴1亄兠r2乮俴亅俴1乯乯
丂亖兠0倁2/俀倓*俿乮兠r1亅兠r2乯
椡偺戝偒偝偼丄兠0倁2/俀倓*俿乮兠r1亅兠r2乯偱偁傞丅
兠r1亜兠r2偺帪丄俴1偑挿偔側傞曽岦傊摥偔丅
丂嫬奅柺偺柺愊偼丄倓俿偱偁傞偐傜丄扨埵柺愊摉傝偺椡倖乮亖俥/倓俿乯偼
倖亖兠0倁2/俀倓2*乮兠r1亅兠r2乯
丂亖兠0乮兠r1亅兠r2乯俤2/俀乮俤偼攠幙撪偺揹奅乯
丂亖俢1俤/俀亅俢2俤/俀乮俤乮亖俤1亖俤2乯偼攠幙撪偺揹奅丄俢偼偦傟偧傟偺攠幙偺揹懇枾搙乯
丂亖俢1俤1/俀亅俢2俤2/俀