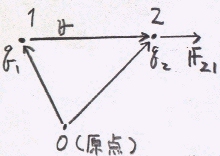

右図において、点1,2に電荷q1、q2がある。この時、q1、q2には、電荷間の距離rの二乗に反比例した力が、 両者を結ぶ方向に働く。この力は、それぞれの電荷量に比例し、同種の電荷の場合には斥力に、異種の電荷の場合には引力になる。 この現象はベクトルによって表現でき、電荷1によって電荷2が受ける力F21は、
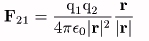
と表される。
ここで、1/(4πε0)は、比例係数である。(ε0:真空中の誘電率 (MKSA単位系で、
r/|r|は、r方向の単位ベクトル(大きさ’1’のベクトル)erを表す。
rを点1、点2の位置ベクトルr1、r2で表せば、
(r=r2-r1)となる。
 上では、一点に存在する電荷が他の点に存在する電荷に及ぼす力をベクトルで表現した。
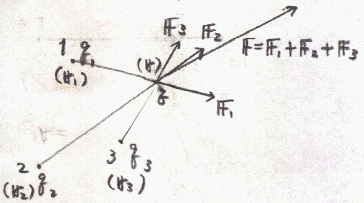
複数の電荷(右図では3つの電荷)が他点に存在する電荷に及ぼす力について考える。
上では、一点に存在する電荷が他の点に存在する電荷に及ぼす力をベクトルで表現した。
複数の電荷(右図では3つの電荷)が他点に存在する電荷に及ぼす力について考える。
点1(r1),2(r2),3(r3)にそれぞれq1,q2,q3の電荷が存在している場合、
他点(r)の電荷qが受ける力F(r)は、(点1,2,3の)それぞれの電荷により受ける力(F1(r)〜F3(r))
のベクトル和になる。式で表せば、
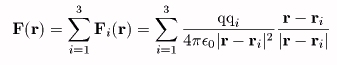
一般にn+1個の電荷が存在するとき、その中の任意の電荷q(位置r,n+1番目の電荷とする)に働く力は、自身(n+1番目の電荷)を除いた個々の電荷による力の’ベクトル’和なので、
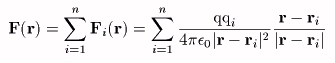
と表現される。ここで、この式を眺めると、力を考えている点rに存在する電荷qがすべての項に含まれている。
そこで、qを括り出すと、
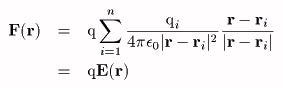
なる表現になる。 Eを電界と呼び数式で表現すれば、上を参考にして
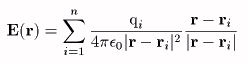
と表現される。着目する場所において、その場所における電界と電荷を掛けることによって力が得られることから、電界とは、 着目する場所において電荷に対してどれだけの力を(どちらの方向に)発生し得るかの程度を表すことが分かる。
複数の電荷が存在する場合には、ある場所における電界は、それぞれの電荷による電界を力と同様にベクトルとして合成すれば求まる。 (おおざっぱに捉えれば、電荷は荷物の重さ、電界はスロープの傾き具合、電荷の受ける力は荷物が落ちて行こうとする力に対応している。)