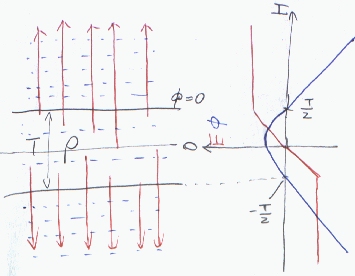
上面が接地された肉厚Tの無限の広がりを持つ平板状に均一に電荷密度ρ(C/m3)で電荷が分布する場合、平面の中心より上下方Hでの電位を求める。
11/11提出期限のレポートで扱った平板状の問題と同様に電界は求まる。
平面に対して垂直な柱を考える。この柱について平面の中心を中心として上下にxの長さで垂直に切り取った柱状の閉曲面を考える。上下面で電界と面は垂直 側面で電界は面と平行なので、電界を積分すると上下面だけが0でない値を取る。また、閉曲面は電荷分布に対して対称なので、 上面下面で電界は(垂直外向きで)同じで、面上で電界の大きさは等しい。 上(下)面の面積をSとすれば、閉曲面内の電荷量は、|x|<T/2のとき2|x|Sρ、|x|>T/2のときTSρとなる。 電界の面積分は2SEである。ゆえに大きさEは
|x|<T/2のとき 2SE=2|x|Sρ/ε0 → E=ρ|x|/ε0
|x|>T/2のとき 2SE=ρTS/ε0 → E=ρT/2ε0
電界は、中心から外に向かう方向。中心から距離に比例して電界は大きくなる。(電気力線が厚さに比例して増加していく。)面の外で電界は一定になる。
面に垂直にx軸を定めてx軸の原点を平面の中心に取って上に向かう方向を正の方向とし電界をベクトル表示すると、y,z軸がどちらを向いても面の中心よりxの位置での電界は、 E(x)=(Ex(x),0,0)とかける。
ただし、Ex(x)=ρ/ε0*x (|x|<T/2)
Ex(x)=ρT/2ε0 (x>T/2)、
Ex(x)=-ρT/2ε0 (x<-T/2)、
上面の電位を基準として(Φ(T/2)=0)Hにおける電位Φ(H)は、電界を積分して
Φ(H)=-∫Ex(x)dx(x;T/2〜H) としてえられる。
T/2<Hのとき
Φ(H)=-∫Ex(x)dx(x;T/2〜H)=-∫ρT/2ε0dx(x;T/2〜H)
=-[(ρT/2ε0*x](x;T/2〜H)
=ρT(T/2-H)/2ε0
-T/2<H<T/2のとき
Φ(H)=-∫Ex(x)dx(x;T/2〜H)=-∫ρ/ε0*xdx(x;T/2〜H)
=-[ρ/2ε0*x2](x;T/2〜H)
=ρ/2ε0*((T/2)2-H2)
H<-T/2のとき
Φ(H)=-∫Ex(x)dx(x;T/2〜H)=-∫ρ/ε0*xdx(x;T/2〜-T/2)+∫ρT/2ε0dx(x;-T/2〜H)
=[ρ/2ε0x2](x;T/2〜-T/2)+[ρT/2ε0*x](x;-T/2〜H)
=ρTH/2ε0+ρ/4ε0T2
=ρT(T/2+H)/2ε0

平面からの距離が同じ点は、同電位になる。その点の集合が等電位面になる。(青の破線)
電気力線は、平面の中心から外に向かって垂直に(電荷が負なら内向きに)まっすぐに伸びる。表面に近づくに連れて電気力線は増えていく。(赤の実線)
電界は一定であるので、電気力線は平行で、それぞれの領域で電気力線の密度は変化しない。