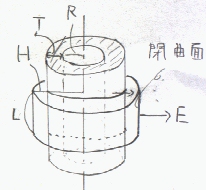
内半径Ｒ、肉厚Ｔ（外半径Ｒ+Ｔ）の無限長円筒状に電荷密度ρ(C/m3)で電荷が分布する場合、円筒の中心から距離Ｈの場所での電界を求める。
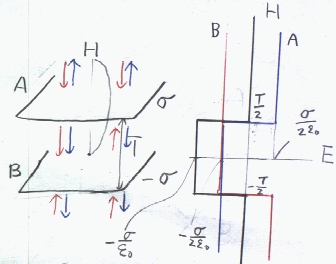
無限の広がりを持つ厚さを無視できるＴの間隔で平行な平面がある。 一方の平面は均一に面電荷密度 σ(C/m2)で電荷が分布し、もう一方の平面は均一に面電荷密度 -σ(C/m2)で電荷が分布する。 平面の中心より面に垂直方向に距離Ｈでの電界を求める。
電界が平行か垂直になるような面を考えることは出来るが、垂直な面上で同じ電界強度になるような閉曲面を考えることは出来ない。
（Ａの上方とＢの下方では電界の方向が異なる。電荷分布に対して対称な閉曲面はない。）
そこで、電界はすべての電荷による電界の合成であることを利用して、電荷をＡ面とＢ面に分けてそれぞれの電界を計算し合成する。
Ａ（Ｂ）面の電界は既に求めてあるので合成すれば、図中のように外部には電界はなく内部に下向きの電界σ/ε0が存在する。
ＡＢ間の電界は一様である。ＡＢ間にしか電界はないことから、Ａよりでた電気力線は、すべてＢへと至ることが分かる。
この問題は、平行平板コンデンサ（電極間の誘電率が、ほとんどの場合真空中とは異なるが）とも類似する。
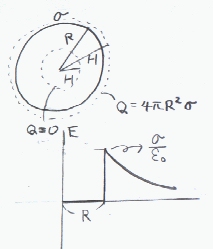
半径Ｒの厚さを無視できる球殻上に均一に面電荷密度 σ(C/m2)で電荷が分布する場合、球殻の中心からＨでの電界を求める。
球殻の中心を中心とする球の閉曲面でガウスの定理を使う。 閉曲面内の電荷は、Ｈ＜Ｒのとき０で Ｈ＞Ｒのとき4πＲ2σ である。 また電界の面積分は（電界は面に垂直で面上で大きさが等しいので）、4πＨ2Ｅである。ゆえに
Ｈ＜Ｒのとき 4πＨ2Ｅ＝０ → Ｅ＝０
Ｈ＞Ｒのとき 4πＨ2Ｅ=4πＲ2σ/ε0 → Ｅ=σＲ2/ε0Ｈ2
電界の方向は、球殻の中心から外向きの方向。
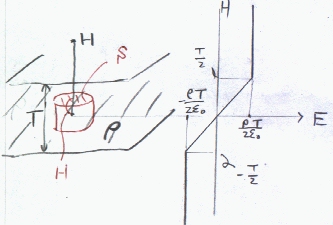
無限の広がりを持つ厚さＴの平面状に均一に電荷密度 ρ(C/m3)で電荷が分布する場合、平面の上方Ｈでの電界を求める。
平面に対して垂直な柱を考える。この柱について平面の中心を中心として上下にＨの長さで垂直に切り取った柱状の閉曲面を考える。上下面で電界と面は垂直 側面で電界は面と平行なので、電界を積分すると上下面だけが０でない値を取る。また、閉曲面は電荷分布に対して対称なので、 上面下面で電界は（垂直外向きで）同じで、面上で電界の大きさは等しい。 上（下）面の面積をＳとすれば、閉曲面内の電荷量は、Ｈ＜Ｔ／２のとき２ＨＳρ、Ｈ＞Ｔ／２のときＴＳρとなる。 電界の面積分は２ＳＥである。ゆえに
Ｈ＜Ｔ／２のとき ２ＳＥ＝２ＨＳρ/ε0 → Ｅ＝ρＨ/ε0
Ｈ＞Ｔ／２のとき ２ＳＥ＝ρＴＳ/ε0 → Ｅ＝ρＴ/２ε0
電界は、中心から外に向かう方向。中心から距離に比例して電界は大きくなる。（電気力線が厚さに比例して増加していく。）面の外で電界は一定になる。
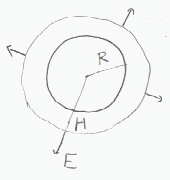
半径Ｒの球内に均一に電荷密度 ρ(C/m3)で電荷が分布する場合、球の中心からＨでの電界を求める。