半径Rの球内に均一に電荷密度 ρ〔C/m3〕で電荷が分布する場合、球の中心からHでの電界を求める。
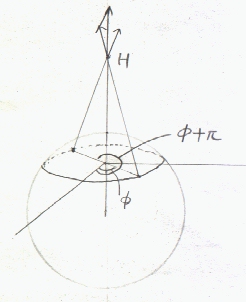
電界は、電荷の分布する球の中心から外に向かう向である。中心からの距離が等しい点では、電界の大きさは同じで、球表面に垂直である。 (r,θ,φで与えられるxyz空間の点(rsinθcosφ,rsinθsinφ,rcosθ)において中心軸に対して反対方向の点(rsinθcos(φ+π),rsinθsin(φ+π),rcosθ)の電荷による電界を考えると、両者によって電界のxy成分は打ち消される。総ての空間内の点において同様に打ち消されるので、電界のx成分、y成分は0となる。電界は、ρ>0のとき、球の中心から外に向かう方向になる。距離の等しいどの点から電荷分布を見ても、電荷分布の見え方は同じである。即ち電界の与えられかた(大きさと、方向の与えられ方)は同じである。電界の与えられ方にも同じ性質がある。(対称性という))
電荷の分布する球を中心にして半径Hの球状の閉曲面上でガウスの定理左辺の面積分を行なう。 右辺の電荷総量も求めて両辺が等しいとおき電界を求める。
閉曲面上での電界の大きさをEとすれば、
左辺=∫E・d S(S:球表面)=∫E・d S(S:球表面)
=E∫d S(Eとd Sは同じ方向で、Eは面上で同じ値)=E4πH2
左辺=E4πH2
右辺=ρ4πH3/3ε0;(H<R)、ρ4πR3/3ε0;(R<H)
左辺=右辺より
H<Rのとき、 E=ρH/3ε0 〔N/C〕 (ρ>0のとき、中心から外に向かう方向)
R<Hのとき、 E=ρR3/3ε0H2 〔N/C〕 (ρ>0のとき、中心から外に向かう方向)
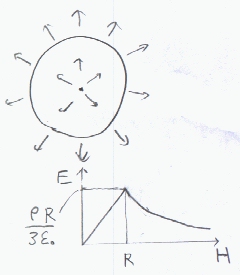
電界は、正電荷なら球の中心から外に向かう(負電荷なら内に向かう)方向になる。電界を図示する。