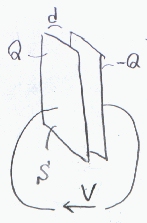
丂柺愊俽偺摫懱斅偑娫妘倓偱暯峴偵抲偐傟偰偄傞丅偦傟偧傟偺摫懱斅偵揹壸俻丄亅俻乮俻亜侽乯傪偨傔偨偲偒摫懱娫偺揹埵嵎倁傪媮傔傞丅 柍尷偺峀偝偺摫懱斅偺寢壥傪嶲峫偵偡傞丅揹奅偼丄摫懱斅偺廃曈晹偐傜棧傟偨拞掱偺摫懱斅娫偱嬒堦偱丄 戝偒偝偼柺揹壸枾搙傪冃偲偡傟偽冃/兠0偱梌偊傜傟傞丅揹奅偼俻偐傜亅俻偵岦偐偆曽岦偱偁傞丅摫懱斅偺廃曈晹偱偼丄 揹婥椡慄偑摫懱斅娫偐傜奜偵偼傒弌傞堊偵丄嬒堦側揹奅偵側偭偰偼偄側偄偑丄廃曈晹偵斾傋偰拞掱偺柺愊偼埑搢揑偵戝偒偄偺偱柺慡懱偑嬒堦側揹奅偵側偭偰偄傞偲傒側偡丅
偝偰丄柺揹壸枾搙偼丄俻/俽偱梌偊傜傟傞偺偱丄揹奅偼俻/兠0俽偲側傞丅椉摫懱斅娫偺揹埑倁偼丄俤倓偱俻偺懁偑崅偄丅
傛偭偰丄惓揹壸偺曽岦偵揹埑偺曽岦傪慖傋偽丄
丂丂倁亖俤倓亖俻/兠0俽*倓
丂丂俻亖兠0俽/倓*倁
偙偺幃偼丄暯峴摫懱斅乮嬌斅乯偵拁愊偡傞揹壸検偲摫懱斅娫偺揹埑偑斾椺偡傞偙偲傪偁傜傢偡丅斾椺掕悢傪'俠'(Capacitance)偱昞偟丄惷揹梕検偲尵偆丅傛偭偰丄
丂丂俠亖佪俻/佪倁亖兠0俽/倓
傕偟丄嬌斅娫偑丄斾桿揹棪兠r偺攠幙偱枮偨偝傟偰偄傟偽丄嬌斅娫偱偼揹懇偑曐懚偝傟傞丅乮傕偪傠傫恀嬻拞偱傕揹懇偺曐懚偼惉棫偟偰偄傞丅乯
嬌斅娫偺揹懇枾搙偺戝偒偝偼丄柺揹壸枾搙俻/俽偵摍偟偄偺偱丄揹奅俤偼丄俻/俽兠0兠r偲側傞丅 傛偭偰嬌斅娫偺揹埑倁偼丄倁亖俤倓亖俻/俽兠0兠r*倓偱昞偝傟傞丅
丂丂俠亖佪俻/佪倁亖兠0兠r俽/倓
乮偙偙偱偼暯峴暯斅偺椺傪偁偘偨偑乯偙偺傛偆偵嬌斅偵揹埑傪報壛偡傞偲嬌斅偵偼揹壸偑拁愊偡傞丅偙偺傛偆側峔憿乮慺巕乯傪僉儍僷僔僞乮僐儞僨儞僒乯偲偄偆丅
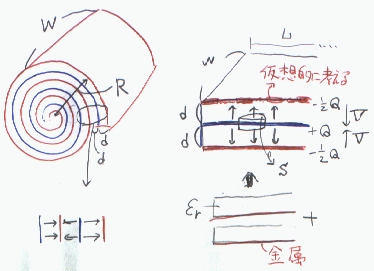 丂塃偺恾偺傛偆偵丄岤偝倓丄暆倂偺斾桿揹棪兠r偺桿揹懱僔乕僩偺曅懁偵旕忢偵敄偄摫懱枌傪枾拝偝偣偨傕偺傪俀枃廳偹偰敿宎俼偺儘乕儖忬偵姫偔丅
偙偺峔憿偼丄俀枃偺摫懱枌娫偵揹埑傪報壛偡傞偲僐儞僨儞僒偲偟偰摥偔丅埲壓偵偙偺峔憿偺惷揹梕検傪媮傔傞丅
丂塃偺恾偺傛偆偵丄岤偝倓丄暆倂偺斾桿揹棪兠r偺桿揹懱僔乕僩偺曅懁偵旕忢偵敄偄摫懱枌傪枾拝偝偣偨傕偺傪俀枃廳偹偰敿宎俼偺儘乕儖忬偵姫偔丅
偙偺峔憿偼丄俀枃偺摫懱枌娫偵揹埑傪報壛偡傞偲僐儞僨儞僒偲偟偰摥偔丅埲壓偵偙偺峔憿偺惷揹梕検傪媮傔傞丅
丂丂俀俽俢亖冃俽丂乮冃偼丄柺揹壸枾搙丂冃亖俻/倂俴亖俀倓俻/兾俼2倂乯
丂丂俢亖冃/俀亖倓俻/兾俼2倂
丂丂俤亖俢/兠0兠r亖倓俻/兾兠0兠r俼2倂
揹嬌娫偺揹埑倁偼丄
丂丂倁亖俤倓亖倓2/兠0兠r兾俼2倂*俻
傛偭偰惷揹梕検丂俠丂偼丄
丂丂俠亖佪俻/佪倁亖兠0兠r兾俼2倂/倓2
丂椺偊偽丄斾桿揹棪兠r亖係丄岤偝倓亖俆侽兪倣丄敿宎俼亖侾噋丄暆倂亖俁噋偲偡傟偽丄俠亖侽.侾俁俁兪俥偲側傞丅
丂桿揹懱撪偵偼丄揹壸乮揹巕丄僀僆儞丄乮懷揹偟偨乯暘巕乯偑嵼傝揹壸偼揹奅偵傛偭偰椡傪庴偗傞丅椡偑尷奅傪墇偊傞偲揹壸偼摦偒弌偟丄桿揹懱枌偼攋夡偝傟傞丅
乮愨墢攋夡乯揹壸偺庴偗傞椡偼揹奅偵斾椺偟丄愨墢攋夡偵帄傞揹奅偼戝偒偔偰侾侽6倁/噋偱偁傞丅
丂丂偙偺桿揹懱枌偵侾侽4倁/噋傑偱偺揹奅傪報壛偟偨偲偡傞偲丄嵟戝報壛揹埑偼丄俆侽倁偲側傞丅
椺偊偽丄偙偆偟偰侽.侾俁俁兪俥丄俆侽倁偺僐儞僨儞僒偑幚尰偱偒傞丅