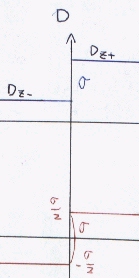
ρT=σ(一定)としてTを限りなく薄くしても(T→0)この結果は変わらない。(電荷の分布する平面の両側で、電束密度の値がσだけステップ状に 変化することになる。)
このときの電束密度の変化を右に示す。
| divE= | ρ-divP ε0 |
と表現されること、ρ-divPが点rに存在する(正味の)電荷密度に相当することを示した。
今、上の式を変形すれば、div は分配則が成り立つので、
div(ε0E+P)=ρ
となる。
div(ε0E+P)=divD=ρ
とかける。ここで、クーロンの法則とガウスの定理の微分表現と積分表現は、
見掛け上数学的な表現は異なるけれども、本質的な(物理的な)意味はすべて同じである。(理論的に互いに等価になる。)
以下の4つの式は、物理的には互いに同等である。
| E(r)= | n Σ i=1 |
qi 4πε0|r-ri|2 | r-ri |r-ri| |
| E(R)= | ∫ dV;r |
ρ(r)dV 4πε0|R-r|2 | R-r |R-r| |
| ∫ | E・dS= | q ε0 | (qは閉曲面S内の全電荷) |
| divE(r)= | ρ(r) ε0 |
よって、上で示したガウスの定理の微分表現と同様に数学的に表現されるDについても(右辺に1/ε0がつかないだけで)同様な関係が成立する。
E→Dに変えて1/ε0を除けば、電束密度についての関係が得られる。
| D(r)= | n Σ i=1 |
qi 4π|r-ri|2 | r-ri |r-ri| | (一様な媒質中でのみ成立する) |
| D(R)= | ∫ dV;r |
ρ(r)dV 4π|R-r|2 | R-r |R-r| | (一様な媒質中でのみ成立する) |
Dには電界と似た性質があることが分かる。
電界に対して電気力線を考えたように D に対しても点電荷qから放射状に伸びる何かを考えることができる。
一様媒質中で、点電荷が一つしかない場合には、この点電荷の場所をr0とし電荷量をq0とすれば、
| D(r)= | q0 4π|r-r0|2 | r-r0 |r-r0| | とかける。 |
電束密度と電荷との関係を簡単に説明する。
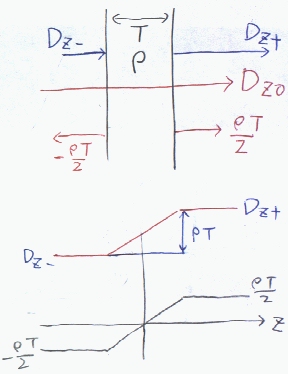
十分に広い厚さTの平面状に密度ρで電荷が分布するとする。平面に垂直にz軸をとり、z軸の基準を厚さの中心とする。 z=−T/2の平面のちょうど外側において電束密度Dは平面に垂直でDz-であるとする。この時、z=T/2における電束密度を求める。
今、平面から放射される電束をガウスの定理を用いて電界のときのように求めると 負の側に−ρT/2 正の側にρT/2となり、方向は、平面に垂直である。
今、負の側の電束密度はDz-であるから今注目する領域の外の電荷によって与えられる電束密度Dz0は、Dz-+ρT/2で平面に垂直である。
(すべての電荷による電束密度を合成した結果Dz-になるのであるから、Dz0-ρT/2=Dz-である。 平面の電荷が変化すれば、左側にも電束が伸びて左の空間の電束密度が変化しようとするが、この変化が起こらないように、 注目する領域の外の電荷分布が変化する(電束に下駄をはかせる)ことが、暗黙の内に示されていることになる。 平面でどのように電荷が分布しても左側の電束密度の分布は一定に保たれるのである。(平面より)左側へ出てゆく電束を打ち消す為に、 これと同じ量の反対向きの電束が加わる(ような追加の電荷分布が考えている領域の外側で起こる)ことになる。 電束は両側に等量出ているので、全電束の半分(左側に加わる電束)だけ、注目する外側の電荷による電束が増加する。 平面の右側では、この電束と平面から出る電束との和だけ(左側に比べて)電束が増加する。この和の電束は、 それぞれが平面から出る電束の半分であるから平面から出る全電束に等しいことが分かる。電界についても同じことがいえる。)
よって正の側の電束密度Dz+は、
Dz+=Dz0+ρT/2で平面に垂直である。ここで、正の側と負の側の電束密度の差を取れば、
Dz+−Dz-=ρT となり、平面の面電荷密度σと等しい。

ρT=σ(一定)としてTを限りなく薄くしても(T→0)この結果は変わらない。(電荷の分布する平面の両側で、電束密度の値がσだけステップ状に
変化することになる。)
このときの電束密度の変化を右に示す。
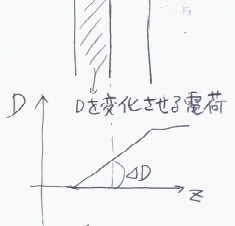
divD(x,y,z)=ρ(x,y,z)の両辺にDの方向の微小移動量ΔTをかければ、 この量は発散の最後の方で述べたように、 移動によってDの方向が変わらなければ、ベクトルDの変化量を与える。つまり、平面を通過するときの平面に垂直な電束密度の変化は、 出会った電荷の量(密度に距離がかかるので面密度になる)に等しいことが分かる。
金属を完全導体と見なせば、帯電した金属では、電荷は表面に面電荷として分布し内部には存在しない。電界、電束密度の方向は金属表面に対して垂直である。よって、
金属内部には電界、電束密度は存在しないので、金属の表面では、電束密度は面に垂直で電束密度は表面の面電荷密度と等しい。
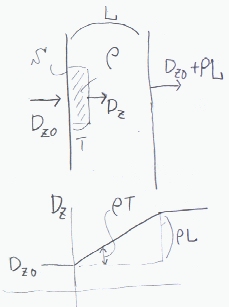
平板の左側で、電束が与えられる時、均一な電荷密度ρの平板内及び平板外の電束密度は、どのように表されるかを考える。
今、厚さT断面積Sの立体を考えると、この立体からでる電束の総量は、ρSTになる。左側では電束の量は、Dz0Sと決められているので、
この立体から出る電束ρSTはTより右へ出てゆく。(左側の電束を一定に保った結果そうなるだけのこと)
よってTの位置での電束は、Dz0S+ρSTである。電束密度Dz=Dz0+ρT=Dz0+σとかける。
σは平板の面電荷密度であるから、電束密度は、面電荷密度だけ増加する。(板の両側の電束密度の差は、面電荷密度に等しい)
電荷密度が厚さ方向にのみ変化する(平板に平行な方向には一様である)とすれば、ρはzのみの一変数の関数になる。
このとき電束密度に対するガウスの法則の微分表現divD=ρは、
dDz/dt=ρ(z)
と表されるので、これをDz(0)=Dz0の条件で解けば、
Dz(Z)=Dz0+∫ρ(z)dz(z;0〜Z)
となる。ρが厚さ方向にも一様であれば、右のような依存性が得られる。