この世に存在するほとんどの物質は、原子から出来ており、原子は正電荷を持つ原子核と負電荷を持つ電子から出来ている。 電気工学で使う材料もすべて、原子から出来ている。このような材料を電界の下においたときの現象について説明する。
原子を構成する原子核と電子は、互いに反対の電荷を持つ為にクーロン力によって引き合っている。この力と電子が原子核の周りを回る 遠心力が釣り合って、正電荷の原子核の周りを負電荷の電子が回る原子が出来ている。 (実際には、原子核の周りに電子の物質波の定在波のようなものが出来ている・・・らしい。)
このような原子では、原子核は点電荷とみなせるが、電子による負電荷は空間でオングストローム(1Å=10-10m)程度で(単独の原子の場合)分布する。 今、電子による負電荷の分布を点電荷とみなせる程度の領域で考えることにする。
固体や液体の場合には、原子核も数オングストローム程度の間隔で並ぶので、'普通のスケール'では、固体や液体は、 正電荷(原子核)も負電荷(電子)も空間に連続的に分布しているとみなしてよい。)
いま、水素原子が、電場中に置かれたとすると、原子核は(正電荷なので)電界の方向に、電子は(負電荷なので)電界とは反対の方向に力を受ける。 互いに逆方向に力を受けることによって、原子核と電子の位置は逆方向にごくわずかにずれる。(原子核と電子の間の力とバランスする。) 正電荷と負電荷がわずかにずれて存在した(変位した)状態になる。正電荷と負電荷の量は(全体として中性(電荷が'0')なので)等しいので、 電気双極子と同じ電界及び電位の分布を与える。
今、正電荷と負電荷のわずかなずれδlは、電界Eに比例する(比例定数をα'とする)とし、ずれた電荷量をqとすれば、電気双極子P'は、
P'=qδl=qα'Eとかける。P'=qα'E=αEとおいて、αを分極率という。
このベクトルは、正電荷が負電荷に対してずれた方向と、ずれた電荷の大きさとずれた距離の積を大きさに持つ。 電気双極子と同じ性質(物理的意味)を持つベクトルである。
物質に電界を及ぼしたとき電気双極子が現れる現象を分極と言う。(水素原子のような分極の現れ方の他に、水のように分子自体に電荷の偏りがある場合には、 外部電界が無い場合には水分子全体として電気双極子が現れていないが、電界の印加によって、水分子の方向が電界の方向に(わずかに)揃おうとして、分極が現れる場合もある。) 分極により生じた電荷にはすべて相手がいる(等量の正負の電荷より構成され、正電荷から出た電気力線の大部分は、相手の負電荷へと入るとみなすことができる)。
固体や液体では、電荷は連続的に分布すると見なすことができるが、電荷密度は一様ではなく、電界に対する変位の大きさも一様ではない。 つまり、分極の大きさは場所により一様とは限らない。 そこで、電荷も変位も均一とみなせるような微小な領域δVについての分極を考え、それを単位体積当りに換算して、電気双極子Pとする。
電荷密度分布をnとすれば、nδV=qなので、
P=P'/δV=qδl/δV=(nδV/δV)δl=nδl
よって、
P=nδl=nα'E=ε0χE(ε0は真空の誘電率)
とかける。χを電気感受率と言う。
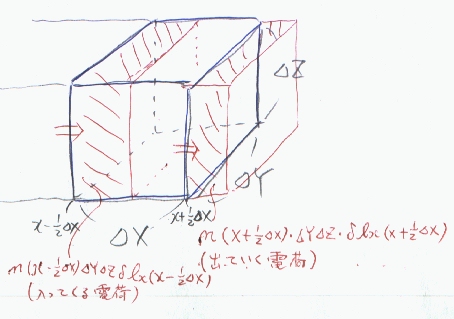
さて、点r(x,y,z)に想定した微小領域ΔXΔYΔZにおいて、電界E(r)によって分極P(r)が起きた時、 この領域内の電荷の量について考える。
分極によってx+1/2ΔXの面を出てゆく電荷量は、n(x+1/2ΔX,y,z)δlx(x+1/2ΔX,y,z)ΔYΔZ
分極によってx-1/2ΔXの面より入る電荷量は、n(x-1/2ΔX,y,z)δlx(x-1/2ΔX,y,z)ΔYΔZ
よって、X軸に垂直な面を通過した電荷による微小領域内の電荷の増加量は、
n(x-1/2ΔX,y,z)δlx(x-1/2ΔX,y,z)ΔYΔZ-n(x+1/2ΔX,y,z)δlx(x+1/2ΔX,y,z)ΔYΔZ
=Px(x-1/2ΔX,y,z)ΔYΔZ-Px(x+1/2ΔX,y,z)ΔYΔZ
ΔXに対して一次で近似すれば、
=∂Px(x,y,z)/∂x*(-1/2ΔX)ΔYΔZ-∂Px(x,y,z)/∂x*(1/2ΔX)ΔYΔZ
=-∂Px(x,y,z)/∂x*ΔXΔYΔZ
同様にY軸、Z軸に垂直な面について考えてたせば、微小領域ΔXΔYΔZ内での分極による電荷の増加量が得られる。すなわち、
分極による電荷の増加量=-(∂Px(x,y,z)/∂x+∂Py(x,y,z)/∂y+∂Pz(x,y,z)/∂z)*ΔXΔYΔZ
=-divPΔXΔYΔZ
ゆえに、単位体積当りの電荷の増加量は、-divPとなる。
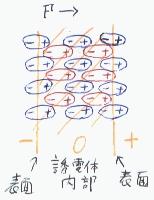
一方、平板の表面では、(例えば、左側表面では、)平板の外に向かって分極による負電荷が誘起されているが、
この電荷をうち消す正電荷を誘起する分極媒質は存在しない。(表面の外側には分極がないのだからそこには分極による正電荷は存在しない。)
この電荷の面密度を求めてみる。上で求めたように、この正味の電荷の体積当たりの増加量をρとすれば、上で求めたように、
ρ=−divP
いま、平板に垂直な成分だけ考えてその方向をz軸にあわせれば、
ρ=−dPz/dz
分極は、表面の極近傍に存在しているので、その領域における面電荷密度σを表せば、
σ=∫ρ(z)dz(z;表面極近傍)=∫(−dPz(z)/dz)dz(z;表面極近傍)=−∫dPz(z)(z;表面極近傍)
=−[Pz(z)](z;表面すぐ外側〜表面すぐ内側)
=−(Pz(表面すぐ内側)−Pz(表面すぐ外側))
=−Pz (平坂内部の単位体積当たりの分極の平板に垂直方向成分をPzとおいた。
表面すぐ外側は、なにもないので分極はない(Pz(表面すぐ外側)=0)
平板のもう一方の側でも面電荷密度を同様にしてもとめれば、 Pz (符号が異なる!)になることが分かる。
内部の単位体積当たりの分極と同量の面電荷が表面に(分極により)誘起していることが分かる。この分極電荷の符号は、分極の起点の側が負、終点の側が正である。
さて、点rには、分極による電荷だけではなく、電界をかける前に分布していた電荷(真電荷、孤立した相手のいない電荷)もある。 この電荷の密度をρとすれば、電界E(r)のもとで点rに存在する(正味の)電荷は、真電荷(孤立電荷:ρ)と分極による電荷(-divP)の和になる。 ここで、ガウスの定理の微分表現divE(r)を思い起こすとdivE(r)は、点rに存在する(正味の) 電荷の密度をε0で割った量であることが理解される。今、点rに存在する(正味の)電荷密度は ρ-divP であるから、分極が存在するときのガウスの定理は、
divE=(ρ-divP)/ε0
と表現される。