電界と電気力線

　電気力線は、ガウスの定理をいかに解釈するかに通じるので、ガウスの定理がよく分からない人は勉強する

電気力線

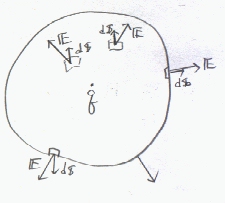
　ガウスの定理は、閉曲面を考えて、その面上のすべての場所において、外に向かう電界の面方向の成分を面積を掛けながら 閉曲面全体にわたって加えると閉曲面内の全電荷量ｑをε_０で割った量になることを示している。(この量は、大きな閉曲面でも 小さな閉曲面でも変わらない。)

いま原点にｑ〔Ｃ〕の電荷が存在する場合の点電荷からｒの位置の電界の式

Ｅ	＝	ｑ		ｒ	〔Ｎ／Ｃ〕　・・・（１）
		４πε０|ｒ|２		|ｒ|

においてｑ／ε_０を括り出して、電界の大きさ（ｒ方向成分）を考えると

｜Ｅ｜＝	ｑ		１	〔Ｎ／Ｃ〕　・・・（２）
	ε０		４π|ｒ|２

と書ける。４π|ｒ|^２は半径|ｒ|〔ｍ〕の球面の表面積を表すので、電荷の中心からｑ/ε₀の量の'何物か'がわきだしており、電界は、わき出して来る'何物か'の面密度に相当すると解釈できる。また、点電荷では、中心から外に向かってわき出した'何物か'は広がってゆくので、 電界の方向は、わきだした'何物か'が向かう方向ともいえる。

複数の電荷がある時には、電界がベクトルの合成で与えられるのと同様に、わきだした'何物か'が総量としてどの密度で、どちらに向かうかが電界を決める。 '何物か'は、正の電荷ではわきだし（生まれ）、負の電荷では消滅する（吸収されていく）。電荷の無い所では、生まれることも消滅することもない。 ガウスの定理は、このような描像として解釈される。

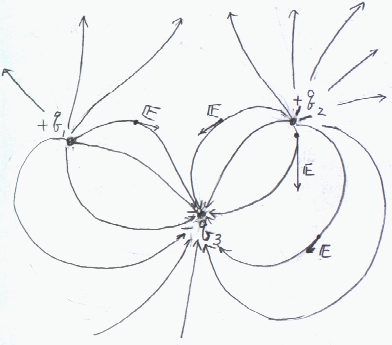
　わきだした'何物か'の一つに注目してどのように移動したかの経路を線で表したのが、電気力線である。 十分な本数の電気力線を描けば、ある場所での電界は、その場所での電気力線の密度が電界の大きさを電気力線の接線の方向が電界の方向を決める。 電荷が大きければ、電気力線のわき出す（吸収されていく）本数は、多くなる。 幾つかの場所で電界の方向を求めて、その場所で電界の方向が接線方向となるような正電荷で生まれる（負電荷で消滅する）曲線を描けば電気力線になる。

右の図では、０＜ｑ_１＜ｑ_２、ｑ_３＜０で、電気力線を書いてある。 電界は、電気力線の接線の方向で与えられる。

これでこの項目は終わり

EL新入生電気磁気学Iのページ

電気磁気学IA要点のコーナーへ戻る

電気磁気学IAへ戻る

電気磁気学I要点のコーナーへ