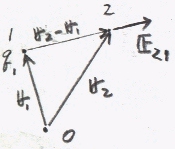
前項で、電界と電荷の積が力になることが分かる。
ここでは、簡単な場合の電界の表現法についてまとめる。

点1(r1)に電荷q1があるとする。
この時、点2(r2)におけるq1による電界E21は、
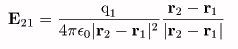
と書ける。これは、電荷間に働く力の表現と同様である。
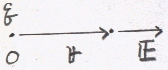
電荷qが原点に存在する時、点rにおける電界は、
q1=q、r2=r、r1=0として
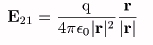
とかける。
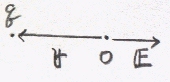
電荷qが点rに存在する時、原点における電界は、
q1=q、r2=0、r1=rとして
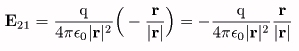
とかける。
点電荷による電界の方向は、正電荷では点電荷の中心から外に向かう方向(負電荷では中心へ向かう方向)になる。
電界の大きさは、距離の二乗に反比例し、比例係数は[
(電荷の大きさと電荷からの距離が電界の大きさを決め、電荷の符号が電界の方向を決めている。)