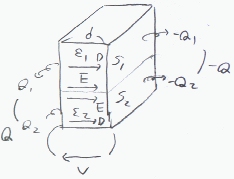
右の図のように比誘電率の異なる誘電体を並べて両側に電極をつけた構造の静電容量を求める。 極板の間隔をdとし、誘電体は、誘電率ε1、面積S1、誘電率ε2、面積S2であるとする。 極板は、導体であるから同電位である。導体間の電圧をVとすれば、電界Eは、極板間で一様であるから、 V=Ed である。
電束は、電界より求まりD1=ε1E、D2=ε2E
よって、それぞれの誘電体に面した極板上の電荷は、
Q1=D1*S1=ε1ES1=ε1S1/d*V
Q2=D2*S2=ε2ES2=ε2S2/d*V
極板上の全電荷Qは、
Q=Q1+Q2=(ε1S1/d+ε2S2/d)*V
C=∂Q/∂V=ε1S1/d+ε2S2/d
上で、ε1S1/dは、誘電率ε1、厚さd、面積S1の平行平板コンデンサの静電容量をあらわす。
同様にε2S2/dは、誘電率ε2、厚さd、面積S2の平行平板コンデンサの静電容量をあらわす。
それぞれをC1、C2とおけば、
C=C1+C2
一般に、コンデンサC1、C2を並列につないだ場合、並列コンデンサを一つのコンデンサCとみなせば、
C=C1+C2
となる。誘電体を並べた構造は、それぞれの誘電体をコンデンサとみなしてコンデンサを並列につないだ場合と同じ静電容量を与える。