内半径Ｒ、肉厚Ｔ（外半径Ｒ+Ｔ）の球殻状に均一に電荷密度 ρ〔Ｃ／ｍ３〕で電荷が分布する場合、球殻の中心からＨでの電界を求める。
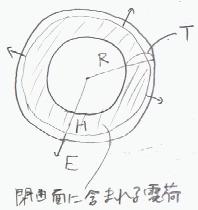
電界は、球の中心より外に向かう方向であるから、電荷の分布する球の中心から外向きに電界の方向はある。
中心からの距離が等しい点では、電界の大きさは同じで、球表面に垂直である。
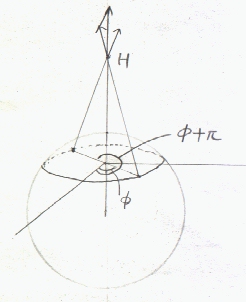（θ，φで与えられる点（ｒsinθcosφ，ｒsinθsinφ，ｒcosθ）において中心軸に対して反対方向の点（ｒsinθcos（φ＋π），ｒsinθsin（φ＋π），ｒcosθ）の電荷による電界を考えると、両者によって電界のｘｙ成分は打ち消される。総ての空間内の点において同様に打ち消されるので、電界のｘ成分，ｙ成分は０となる。ρ＞０なら、電界は球の中心から外に向かう方向になる)
電荷の分布する球を中心にして半径Ｈの球状の閉曲面上でガウスの定理左辺の面積分を行なう。
右辺の電荷総量も求めて両辺が等しいとおき電界を求める。
閉曲面上での電界の大きさをＥとすれば、
左辺＝∫Ｅ・d Ｓ（Ｓ：球表面）＝∫Ｅ・d Ｓ（Ｓ：球表面)
＝Ｅ∫d Ｓ（Ｅとd Ｓは同じ方向で、Ｅは面上で同じ値）＝Ｅ４πＨ２
左辺＝Ｅ４πＨ２
右辺＝０(Ｈ＜Ｒ)、ρ４π(Ｈ３-Ｒ３)／３ε０；（Ｒ＜Ｈ＜Ｒ+Ｔ）、ρ４π（（Ｒ＋Ｔ）３−Ｒ３）／３ε０；（Ｒ＋Ｔ＜Ｈ）
左辺＝右辺より、
Ｈ＜Ｒのとき、 Ｅ＝０ 〔Ｎ／Ｃ〕
Ｒ＜Ｈ＜Ｒ＋Ｔのとき、 Ｅ＝ρ（Ｈ３−Ｒ３）／３ε０Ｈ２ 〔Ｎ／Ｃ〕 （ρ＞０のとき中心から外に向かう方向）
Ｒ＋Ｔ＜Ｈのとき、 Ｅ＝ρ（（Ｒ＋Ｔ）３−Ｒ３）／３ε０Ｈ２ 〔Ｎ／Ｃ〕 （ρ＞０のとき、中心から外に向かう方向）
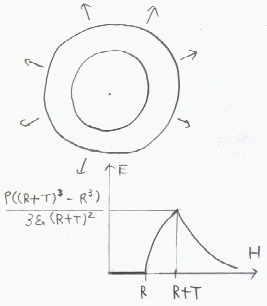
電界は、球の中心から外に向かう（負の電荷なら内に向かう）方向になる。電界を図示する。