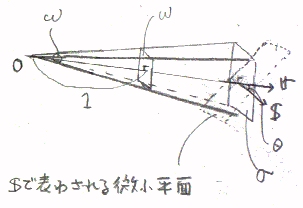
丂塃偺恾偵偍偄偰丄揰俷偐傜倰偺埵抲偵偁傞旝彫暯柺傪峫偊傞丅
丂偙偺暯柺偼丄戝偒偝偑旝彫暯柺偺柺愊丄曽岦偑旝彫暯柺偵悅捈側曽岦傪梌偊傞儀僋僩儖俽偱昞尰偝傟傞丅
丂揰俷偐傜偼丄旝彫暯柺俽偼丄俽偺倰曽岦惉暘偟偐擣幆偝傟側偄偺偱丄
丂旝彫暯柺俽偺戙傢傝偵旝彫暯柺俽偺倰曽岦惉暘冃傪峫偊傞丅乮揰俷偐傜尒偰擣幆偱偒傞柺愊乯
丂俽偲倰偺側偡妏傪兤偲偡傟偽丄倕倰傪倰曽岦偺扨埵儀僋僩儖偲偟偰丄
丂丂丂冃亖|俽|cos兤丂乮亖俽丒倕倰亖俽丒倰/|倰|乯
丂偲側傞丅
丂丂偙偙偱丄冃偵偮偄偰峫偊傞丅
丂冃偼|倰|2偵斾椺偡傞偺偱丄斾椺掕悢傪冎偲偡傞偲
丂丂丂冃亖冎|倰|2
丂偲昞尰偱偒傞丅
丂冎傪棫懱妏偲偄偄丄尨揰偵偍偄偰帇栰偺峀偑傝嬶崌偵憡摉偡傞丅
丂傑偨丄冎偼丄揰俷偲旝彫暯柺俽傪寢傫偱偱偒傞峀偑偭偰偄偔悕嬋柺偑丄敿宎'侾'偺媴柺偐傜愗傝庢傞柺偺柺愊偱傕偁傞丅
丂乮傕偪傠傫旝彫暯柺俽偺宍偼擟堄偱偁傞偐傜丄冎傗冃偺宍忬傕擟堄偱偁傞丅摨偠戝偒偝傪帩偮冎偵懳偟偰
柍悢偺宍忬偺冎偑懚嵼偡傞丅冃偼丄娵偱傕巐妏偱傕嶰妏偱傕丒丒丒偱傕丄摨偠冎傪梌偊偆傞丅乯
丂冎偺扨埵偼 steradian (僗僥儔僕傾儞)偱偁傞丅
丂媴偺昞柺愊偼丄4兾俼2偱偁傞偐傜丄俁師尦偺暵嬋柺傪撪晹偐傜偺偧偄偨偲偒偺暵嬋柺偺棫懱妏冎偼丄
丂4兾俼2亖冎俼2丂丂傛傝丄
丂冎亖4兾丂偲側傞丅
乮敿宎 '1' 偺媴昞柺偺偡傋偰傪偲傞偺偱偁傞偐傜敿宎 '1' 偺媴柺偺昞柺愊係兾偵側傞丅乯
丂偁傞応強傪婎弨偵偟偰丄埵抲倰偵偁傞廫暘偵彫偝側柺嚈俽 偲 偦偺棫懱妏嚈冎偲偺娭學偼丄
丂
| 嚈冎亖 | 侾 乥倰乥俀 | 嚈冃亖 | 侾 乥倰乥俀 | 嚈俽丒倰 乥倰乥 |
丂偱梌偊傜傟傞丅尨揰傪娷傓暵嬋柺偱椉曈傪愊暘偡傟偽丄
丂
| 佺 | d 冎亖 |
佺 | 侾 乥倰乥俀 | 倰 丒d 俽乥倰乥 |
丂嵍曈偑係兾偱偁傞偙偲傪峫椂偟偰曄宍偡傟偽丄
| 佺 | 侾 係兾乥倰乥俀 | 倰 乥倰乥 | 丒d 俽亖侾 |
偙偺娭學偼丄僈僂僗偺掕棟偱棙梡偡傞丅