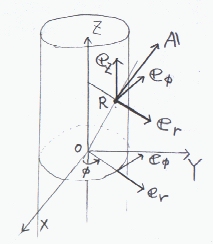

右図のように、X,Y,Z軸で与えられる空間に点R(x,y,z)(X,Y,Z軸の原点OとRを結ぶベクトルはR=(x,y,z)となる。)を考え、 点Rにおける任意ベクトルA(x,y,z)(=A(R))の円柱座標によるベクトル表現について考える。
まず、点Rを側面に含むZ軸方向に向いた円柱を考える。円柱をZ軸の正の方向から眺めると点Rは、XY面内に与えられる。 この面内で円柱の半径(Z軸と点Rとの距離)をr、Z軸(XY面の原点)と点Rを結ぶ線のX軸からみた角度をφとすると、 点Rは(x,yの二変数の代わりに)r,φの二変数によっても与えられる。
zの変数はそのまま用いて、点Rはr,φ,zの三変数によっても(x,y,zを用いるのと同様に)一意に与えられることがわかる。
今それぞれの変数に対応した単位ベクトルを考える。rの増加する方向(er)、とφの増加する方向(eφ)と、
zの増加する方向(ez)は、図中の方向になるので互いに直交することが分かる。ezの方向は、
erからeφへと右ねじを右に回した時に進む方向になっている。
(外積の表現を使えば、ez=er×eφで、
er、eφ、ezの順で右手系の座標系になる。)
よって、図中で示したer,eφ,ezが(r,φ,z)で点を表すときのそれぞれの変数の座標軸の方向を表す。
三次元空間の点Rを(r,φ,z)で表し、その点で与えられるベクトルA(R)(=A(r,φ,z))をer,eφ, ez方向(r,φ,z軸)の成分に分解して A=(Ar,Aφ,Az)と表現するのが、円柱座標系である。
(この座標系では、xyz座標系と違って、r軸とφ軸の方向(erとeφ)は場所によって異なり、
er(φ),eφ(φ)のように、φの関数となる。)
ここで、xyz座標と円柱座標の関係を示す。図より、xy平面内の変数変換は、
x=rcosφ、y=rsinφ
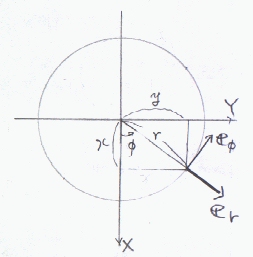
逆にとけば、
r=(x2+y2)1/2
φ=Tan-1(y/x)(0<x),φ=Tan-1(y/x)+π (x<0)
xyz座標で表して、
∂R/∂r=(cosφ、sinφ、0)
∂R/∂φ=(-rsinφ、rcosφ、0)=r(-sinφ、cosφ、0)
であるので、座標軸の方向の単位ベクトルは、
er=cosφex+sinφey
eφ=-sinφex+cosφey
逆に解いて、
ex=cosφer-sinφeφ
ey=sinφer+cosφeφ
と表される。
| ⊿R= | ∂R ∂r | ⊿r+ | ∂R ∂φ | ⊿φ+ | ∂R ∂z | ⊿z |
eφの方向は、erをπ/2回転させた方向(円の接線方向)と一致している。
(cos(φ+π/2)ex+sin(φ+π/2)ey=eφとなっている。)
A=Arer+Aφeφ+Azez
=Ar(cosφex+sinφey)+Aφ(-sinφex+cosφey)+Azez
=(Arcosφ-Aφsinφ)ex+(Arsinφ+Aφcosφ)ey+Azez
=Axex+Ayey+Azez
これが、xyz座標と円柱座標のベクトル成分相互の関係となる。
(単位ベクトルにかかる係数がそれぞれの軸方向の成分を表す。)
Ax=Arcosφ-Aφsinφ
Ay=Arsinφ+Aφcosφ