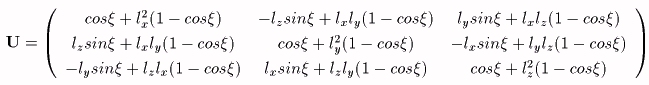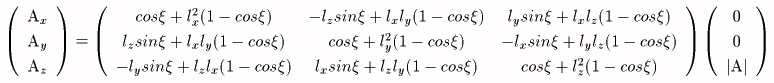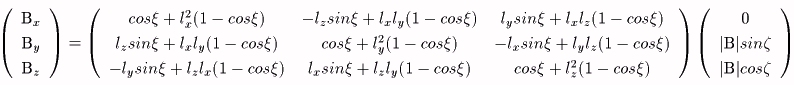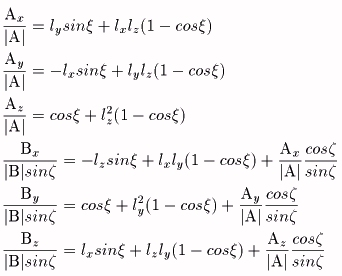このページは、
Friday, 10-Dec-2004 23:35:06 JSTに更新されました。
このページは、’後藤 英雄@電気システム工学科 中部大学’が作成しています。
連絡は、後藤@電気システム工学科へお願いします。
電気工学で使う数学的手法 presented since 1996
ベクトルの外積
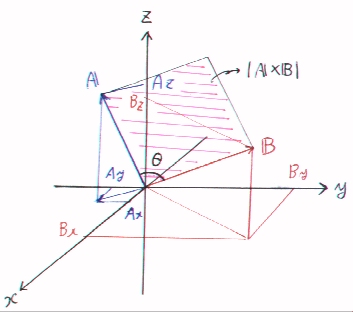
右の図において、ベクトルA(=(Ax,Ay,Az))と
B(=(Bx,By,Bz))を考える。
ただし、A、Bとも始点はOにあるとする。
このとき、次のような成分で表されるベクトルをA×Bと表現し、ベクトルA、Bの外積という。
A×B=(AyBz−ByAz,
AzBx−BzAx,AxBy−BxAy)
このベクトルは、単位ベクトルex,ey,ezを使えば、
A×B=(AyBz−ByAz)ex
+(AzBx−BzAx)ey
+(AxBy−BxAy)ez
と表現され、3×3の行列の行列式の計算を記号的に用いれば、次のようにも表される。
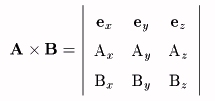
以下に、外積の性質(ベクトルの大きさ、方向、など)について説明する。
αをスカラとすると、αA=(αAx,αAy,αAz)となるので、
上の成分の計算式を参考にして変形すれば、
(αA)×B
=(αAyBz−ByαAz)ex
+(αAzBx−BzαAx)ey
+(αAxBy−BxαAy)ez
=α((AyBz−ByAz)ex
+(AzBx−BzAx)ey
+(AxBy−BxAy)ez)
=α(A×B)
上の成分の計算式を参考にして B×A を求める。
B×A
=(ByAz−AyBz,BzAx−AzBx
,BxAy−AxBy)
=−(AyBz−ByAz,AzBx−BzAx
,AxBy−BxAy)
=−A×B
よって、B×A=−A×B (交換すると符号が変わる。)
C=(Cx,Cy,Cz)とし、(A+C)×Bを計算する。
A±C=(Ax±Cx,Ay±Cy,Az±Cz)より、
先の計算のベクトル表現を参考にして、
(A±C)×B
=((Ay±Cy)Bz−By(Az±Cz))ex
+((Az±Cz)Bx−Bz(Ax±Cx))ey
+((Ax±Cx)By−Bx(Ay±Cy))ez
=(AyBz−ByAz)ex
+(AzBx−BzAx)ey
+(AxBy−BxAy)ez
±((CyBz−ByCz)ex
+(CzBx−BzCx)ey
+(CxBy−BxCy)ez)
=A×B±C×B
よって、(A±C)×B=A×B±C×B (分配則が成り立つ。)
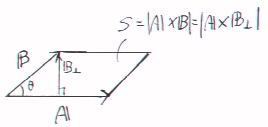
上で、B=aA、C=0 とおいて、A×(aA)を計算すると、
(aA)×A=aA×A=0 となる。
平行なベクトルの外積は0である。(一方のベクトルを他方のベクトルに対して平行な成分と垂直な成分に分解して、分配則も用いれば、
任意の二つのベクトルの外積は、二つのベクトルの互いに直交する成分のみで決まることが分かる。)
外積の大きさについて考える。
ベクトルA、Bのなす角をθとすれば、内積を使って、cosθ=A・B/|A||B|であるので、
sin2θ=1−cos2θ=1−(A・B/|A||B|)2 より、
(|A||B|sinθ)2=(|A||B|)2−(A・B)2
=((Ax2+Ay2+Az2)
(Bz2+By2+Bz2))
−(AxBx+AyBy+AzBz)2
=(AxBy)2+(AxBz)2
+(AyBx)2+(AyBz)2
+(AzBx)2+(AzBy)2
−2(AxBxAyBy+AyByAzBz
+AzBzAxBx)
=(AxBy)2+(AyBx)2−2AxBxAyBy
+(AyBz)2+(AzBy)2−2AyByAzBz
+(AzBx)2+(AxBz)2−2AzBzAxBx
=(AxBy−AyBx)2
+(AyBz−AzBy)2+(AzBx−AxBz)2
この式を外積の成分と比較すれば、第一項は外積A×Bのz成分の2乗、第2項はx成分の2乗、第3項はy成分の2乗になっている。よって、この式は、(外積を表す)ベクトルA×Bの大きさの2乗を表すことが分かる。ゆえに、
(|A||B|sinθ)2=|A×B|2
0≦θ≦π とすれば、
|A||B|sinθ=|A×B|
ここで、|A||B|sinθは、AとBを二辺とする平行四辺形の面積に相当するので、
外積 A×B の大きさは、ベクトルAとBを二辺とする平行四辺形の面積を表すことが分かる。
外積の方向について考える。
 外積の成分を参考にして、(A×B)・Aを計算する。
外積の成分を参考にして、(A×B)・Aを計算する。
(A×B)・A=((AyBz−ByAz)ex
+(AzBx−BzAx)ey
+(AxBy−BxAy)ez))
・(Axex+Ayey+Azez)
=(AyBz−ByAz)Ax
+(AzBx−BzAx)Ay
+(AxBy−BxAy)Az
=Bz(AyAx−AxAy)
+By(AzAx−AxAz)
+Bx(AzAy−AyAz)=0
(A×B)・A=0 同様にして、(A×B)・B=0
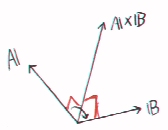
ゆえに、外積A×BはベクトルAおよび、Bに垂直であることが分かる。
A×Bは、A、Bを位置ベクトルとしたとき、二つのベクトルを含む平面に垂直な方向になっている。
(平面に垂直な方向は、平面に裏表があるように二つの方向がある(一方をhとすれば、−hの方向)。
下で示すようにA×Bの方向は、Aの方向からBの方向へ
鋭角で’右ねじを’回転したとき、右ねじの進む方向になっている。)
(言葉を換えれば、AとBの始点をそろえて空間においたとき、自身が始点に立ったとき、それぞれのベクトルを矢に見立てて、
’左手でAの矢’を’右手でBの矢’を握ったとき’体の向いている方向’がA×Bの方向
(×記号の左側のベクトルを左手に右側のベクトルを右手に握ったとき体の向いている方向)である。)
外積A×Bは、A,Bを位置ベクトルと見立てたとき、大きさが辺A、Bからなる平行四辺形の面積、
方向がA、Bの作る平面に垂直で、AからBへ右ねじを回して進む方向のベクトルを表す。
(A、Bを用いた成分は、先に表した。)
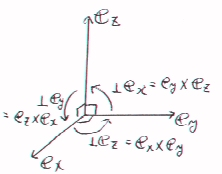 平面において単位ベクトルexとeyに垂直な方向は、面の表側と面の裏側に対応して二つの方向がある。
このどちらかの方向に第三軸を選べば、空間を表す座標に対する単位ベクトルの組ができる。平面に座標を表すベクトルを設定したときに
第一の座標を表すベクトルをex、第二の座標を表すベクトルをeyと仮におけば、
exからeyへ右ねじを回したとき進む方向(外積ex×eyの与える方向)
で面の表裏は一意に決定される。面の表側を外積の与える方向とし、この方向に座標の第三軸(例えば、ez)を割り当てる座標系を右手系という。(こうなるように外積を定義した。)
平面において単位ベクトルexとeyに垂直な方向は、面の表側と面の裏側に対応して二つの方向がある。
このどちらかの方向に第三軸を選べば、空間を表す座標に対する単位ベクトルの組ができる。平面に座標を表すベクトルを設定したときに
第一の座標を表すベクトルをex、第二の座標を表すベクトルをeyと仮におけば、
exからeyへ右ねじを回したとき進む方向(外積ex×eyの与える方向)
で面の表裏は一意に決定される。面の表側を外積の与える方向とし、この方向に座標の第三軸(例えば、ez)を割り当てる座標系を右手系という。(こうなるように外積を定義した。)
実際計算してみてもex×ey=ezになっていることが確認される。
(上で、(1,0,0)と(0,1,0)の外積を計算すればよい。ノートにx軸とy軸を描くとノートの表面から自分の方に、z軸が伸びている。)
図より簡単に、ey×ez=ex、
ez×ex=eyになっていることが分かる。
(x,y,zに関して循環している)実際計算しても容易に確認される。
他の座標表現においても右手系になっている。
例えば、円柱座標では、er×eφ=ez
極座標では、 er×eθ=eφ
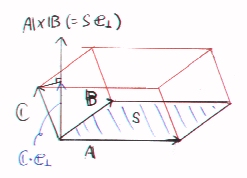
平行六面体の体積
位置ベクトル A,B,Cを辺とする平行六面体を考える。この平行六面体の体積は、辺A,Bからなる平行四辺形の面積に
辺Cによって与えられる高さを掛ければよい。辺A,Bからなる平行四辺形の面積をS平行四辺形に垂直な方向の単位ベクトルをe⊥とすれば、先ほどの外積の性質により、
A×B=Se⊥
平行六面体の体積Vは、CのA,Bに対する垂直成分がC・e⊥であるから、
V=SC・e⊥=C・Se⊥=C・(A×B)
V=C・(A×B)=(A×B)・C
もしこの値が負になるときは、Cのe⊥方向成分が負であることから、内積の性質によりCベクトルがA,Bの作る面の裏面に成分を持つことが分かる。
(A,B,Cの順序にとると左手系になっているということ。このときには、B,A,Cの順序にとれば右手系になっている。図から分かるように、B×Aをとれば面の表がCの側になるので、Vは正になる。)
平行四辺形をB、C またはC、Aで作ってもよいので、同様にしてVを求めて正負で分けて分類すれば、
V=(A×B)・C=(B×C)・A=(C×A)・B
が一つの組になる。
A、B、C が右手系の関係になっていれば、上の体積は正。左手系の関係になっていれば、上の体積は負になる。
A,B,Cを辺とする平行六面体の体積は、(A×B)・Cであらわされ、この値の正負は、
A,B,Cベクトル相互の方位関係(右手系になっているか?左手系になっているか?を表す。
もし負になっていれば、B,A,Cが右手系になっていることを示す。
一般に座標は、右手系になるように選ぶので、座標軸を表すベクトルで、このような計算を行えば(直交座標系なら大きさは1で)正の値になっているはずである。
(第一軸×第二軸の外積により第三軸を決めるのであるから当然である。)
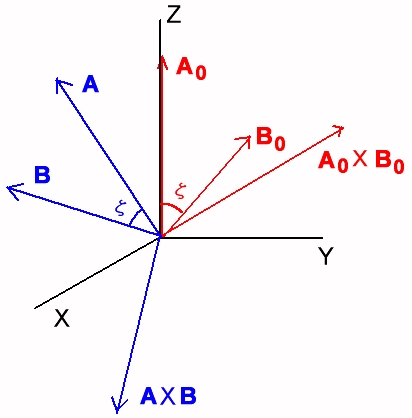
A×Bが、AからBへ右ねじを回したときにねじの進む方向になっていることの説明
外積A×BとA、Bの方向の関係について考えるために、A、Bベクトルを考えやすい方向へ回転する。
A、Bにおいて、AとBのなす角は0又はπでないとする。
ベクトルの回転を表す行列において、Aをz軸へ、Bをyz面内へ変換する変換行列を考える。
Aのz軸へ変換した後のベクトルA0の成分は、大きさは変わらないので(0,0,|A|)、Bのyz面内へ変換した後のベクトルB0の成分は、同様にして、(0,|B|sinζ,|B|cosζ)とおける。(ζはベクトルAとBのなす角である。)
ここで、A→A0、B→B0の変換を表す行列を求める。
回転行列は、elを回転軸にして、ある角度(ξ)の回転によって、上のベクトルの変換を起こす。elを軸にして−ξの回転を行えば、ベクトルは元に戻るはずである。よって、A0→A、B0→Bの変換行列の回転角ζの符号を変えれば求める変換行列になる。
A0→A、B0→Bの変換行列を求める。
変換行列は次のように表される。
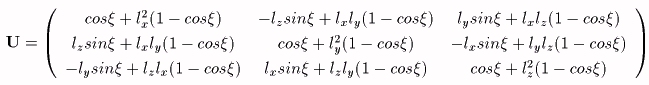
lx2+ly2+lz2=1である。この行列の成分には、次の関係がある。
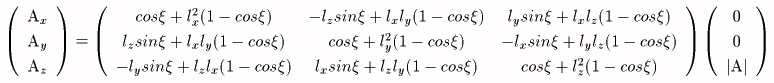
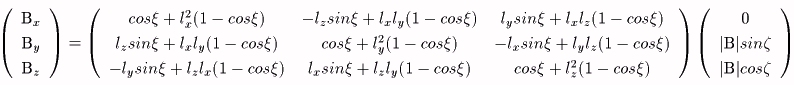
これより、lx、ly、lz、ξ、ζ、とA、Bの成分の関係は、次のようになる。
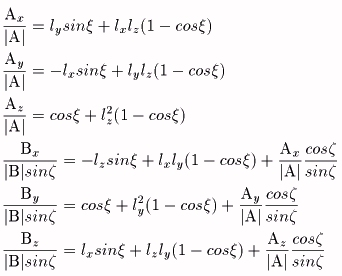
これらの式より、lx、ly、lz、ζ、ξを求めることができる。
こうして得られた回転変換により、A、Bより、A0、B0を得て、A0×B0(=C0)を求めれば、A0,B0、C0の関係は、A、B、Cの関係と等しい。そこで、C0のA0、B0との関係について考える。
成分で考えれば、外積の定義より、
C0=(−|A||B|sinζ,0,0)
このベクトルは、もし、|B|sinζ(B0のy成分)が正ならx軸の負の方向を向き、|B|sinζが負ならx軸の正の方向を向くことが分かる。
この結果より、外積の方向は、A0からB0に右ねじを(鋭角に)回したときに右ねじの進む方向と一致することが分かる。
A、B、A×Bにも同様の関係があることから、一般に外積A×Bの方向は、
A,Bにより作られる面に垂直でAからBへ右ねじを右に回したときにねじの進む方向
(始点に立って、Aを左手にBを右手に掴んだとき体の向いている方向)であるといえる。
これでこの項目は終わり
電気工学で使う数学的手法の入り口ページ
ページの選択
井戸・田橋+後藤 研究室トップページ
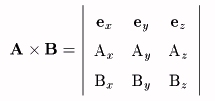

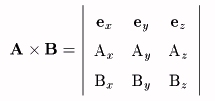
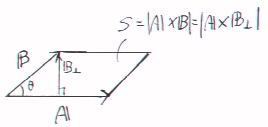
 外積の成分を参考にして、(A×B)・Aを計算する。
外積の成分を参考にして、(A×B)・Aを計算する。
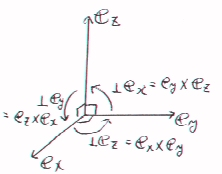 平面において単位ベクトルexとeyに垂直な方向は、面の表側と面の裏側に対応して二つの方向がある。
このどちらかの方向に第三軸を選べば、空間を表す座標に対する単位ベクトルの組ができる。平面に座標を表すベクトルを設定したときに
第一の座標を表すベクトルをex、第二の座標を表すベクトルをeyと仮におけば、
exからeyへ右ねじを回したとき進む方向(外積ex×eyの与える方向)
で面の表裏は一意に決定される。面の表側を外積の与える方向とし、この方向に座標の第三軸(例えば、ez)を割り当てる座標系を右手系という。(こうなるように外積を定義した。)
平面において単位ベクトルexとeyに垂直な方向は、面の表側と面の裏側に対応して二つの方向がある。
このどちらかの方向に第三軸を選べば、空間を表す座標に対する単位ベクトルの組ができる。平面に座標を表すベクトルを設定したときに
第一の座標を表すベクトルをex、第二の座標を表すベクトルをeyと仮におけば、
exからeyへ右ねじを回したとき進む方向(外積ex×eyの与える方向)
で面の表裏は一意に決定される。面の表側を外積の与える方向とし、この方向に座標の第三軸(例えば、ez)を割り当てる座標系を右手系という。(こうなるように外積を定義した。)