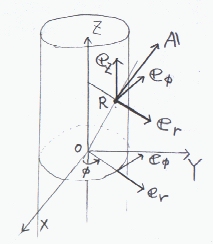
円柱座標の座標変数に対する単位ベクトルは、xyz座標に対して次のような変換により与えられる。
er=cosφex+sinφey
eφ=-sinφex+cosφey
ez=ez
座標軸を表す単位ベクトルはφのみの関数であるから、φについての微分だけ0でない。よって、座標変数に対する微分は次のようになる。
∂er/∂φ=−sinφex+cosφey=eφ
∂eφ/∂φ=−cosφex−sinφey=−er
∂ez/∂φ=0
あらためて書けば、
| ∂er ∂φ | =eφ |
| ∂eφ ∂φ | =−er |
| ∂ez ∂φ | =0 |
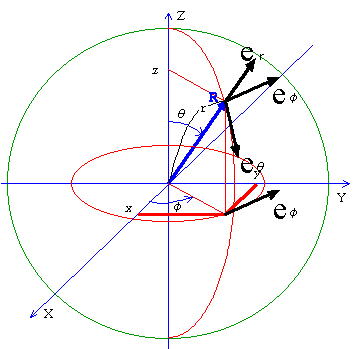
極座標の座標変数に対する単位ベクトルは、xyz座標に対して次のような変換により与えられる。
er=sinθcosφex+sinθsinφey+cosθez
eθ=cosθcosφex+cosθsinφey-sinθez
eφ=-sinφex+cosφey
座標軸を表す単位ベクトルはθとφの関数であるから、θとφについての微分だけ0でない。よって、座標変数に対する微分は次のようになる。
∂er/∂θ=cosθcosφex+cosθsinφey-sinθez
=eθ
∂eθ/∂θ=−sinθcosφex−sinθsinφey−cosθez
=−(sinθcosφex+sinθsinφey+cosθez)=−er
∂eφ/∂θ=0
∂er/∂φ=sinθ(−sinφex+cosφey)=sinθeφ
∂eθ/∂φ=cosθ(−sinφex+cosφey)=cosθeφ
∂eφ/∂φ=−cosφex−sinφey
=−(cosφex+sinφey)
ここで、sinθer+cosθeθ=cosφex+sinφeyであるから、
∂eφ/∂φ=−(sinθer+cosθeθ)
あらためて書けば、
| ∂er ∂θ | =eθ |
| ∂eθ ∂θ | =−er |
| ∂eφ ∂θ | =0 |
| ∂er ∂φ | =sinθeφ |
| ∂eθ ∂φ | =cosθeφ |
| ∂eφ ∂φ | =−(sinθer+cosθeθ) |