丂丂椡偼丄慄偐傜悅捈偵奜偵岦偐偆曽岦偱丄侾.俉倃侾侽侾侽乛俫乲俶乴
嘋丂嘊偵偍偄偰丄揹婥椡慄傪昤偗丅
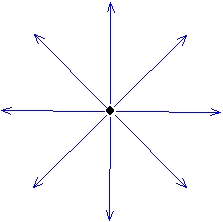
丂埲壓偺栤戣偵偮偄偰摎偊傛丅昁梫側傜嵗昗傪揔摉偵愝掕偟偰傛偄丅
I丂懢偝偺柍帇偱偒傞慄忬偵扨埵挿偝摉偨傝兩乲C乛倣乴偱揹壸偑暘晍偟偰偄傞丅
嘆丂慄偐傜悅捈曽岦偵俫乲倣乴偺埵抲偱偺揹奅傪媮傔傛丅
夝愢偺儁乕僕傪嶲峫偵偟偰丄僈僂僗偺掕棟傪巊偆丅揹奅偼丄慄偐傜悅捈偵奜傊岦偐偆乮兩亜0偺偲偒乯 乮揰偐傜悅捈偵慄偵岦偐偆乮兩亙0偺偲偒乯乯曽岦傪岦偔丅
| 丂丂俤亖丂 | 兩 俀兾兠侽俫 | 乲倁乛倣乴 |
俥亖俻俤偱偁傞偐傜丄揹奅偲摨偠曽岦偵椡偼摥偔丅乮俻亙侽偺偲偒偼丄揹奅偲偼媡曽岦偵椡傪庴偗傞丅乯
| 丂丂俥亖丂 | 兩俻 俀兾兠侽俫 | 乲俶乴 |
丂丂揹奅偼丄慄偐傜悅捈偵奜偵岦偐偆曽岦偱丄侾.俉倃侾侽侾侽乛俫乲倁乛倣乴
丂丂椡偼丄慄偐傜悅捈偵奜偵岦偐偆曽岦偱丄侾.俉倃侾侽侾侽乛俫乲俶乴
嘋丂嘊偵偍偄偰丄揹婥椡慄傪昤偗丅

II丂敿宎俼侾乲倣乴偺岤偝傪柍帇偱偒傞墌摏侾偲敿宎俼俀乲倣乴偺岤偝傪柍帇偱偒傞墌摏俀偑摨幉忬偵偁傞丅
乮俼侾亙俼俀乯
墌摏侾偵扨埵柺愊摉偨傝冃侾乲俠乛倣俀乴偺揹壸丄墌摏俀偵扨埵柺愊摉偨傝冃俀乲俠乛倣俀乴偺揹壸偑暘晍偟偰偄傞丅
嘆丂墌摏偺拞怱偐傜奜曽岦偵俫乲倣乴偺埵抲偱偺揹奅傪媮傔傛丅
夝愢偺儁乕僕傪嶲峫偵偟偰丄僈僂僗偺掕棟傪巊偆丅揹奅偼丄拰偺拞怱幉偵懳偟偰悅捈側曽岦偵側傞丅
| 俫亙俼侾偺偲偒丂丗 | 丂丂俤亖侽乲倁乛倣乴 |
| 俼侾亙俫亙俼俀偺偲偒丂丗 | 丂丂俤亖 | 俀兾俼侾冃侾 俀兾兠侽俫 | 亖 | 俼侾冃侾 兠侽俫 | 乲倁乛倣乴 |
| 俼俀亙俫偺偲偒丂丗 | 丂丂俤亖 | 俀兾俼侾冃侾亄俀兾俼俀冃俀 俀兾兠侽俫 | 亖 | 俼侾冃侾亄俼俀冃俀 兠侽俫 | 乲倁乛倣乴 |
俥亖俻俤偱偁傞偐傜丄揹奅偲摨偠曽岦偵椡偼摥偔丅乮俻亙侽偺偲偒偼丄揹奅偲偼媡曽岦偵椡傪庴偗傞丅乯
| 俫亙俼侾偺偲偒丂丗 | 丂丂俥亖侽乲俶乴 |
| 俼侾亙俫亙俼俀偺偲偒丂丗 | 丂丂俥亖 | 俀兾俼侾冃侾俻 俀兾兠侽俫 | 亖 | 俼侾冃侾俻 兠侽俫 | 乲俶乴 |
| 俼俀亙俫偺偲偒丂丗 | 丂丂俥亖 | 乮俀兾俼侾冃侾亄俀兾俼俀冃俀乯俻 俀兾兠侽俫 | 亖 | 乮俼侾冃侾亄俼俀冃俀乯俻 兠侽俫 | 乲俶乴 |
| 丂俫亙俼侾丂 | 丂俼侾亙俫亙俼俀丂 | 丂俼俀亙俫丂 | 揹婥椡慄 | |
| 揹丂奅乲俶乛俠乴丗丂 | 侽 | 侾.侾亊侾侽俋乛俫 | 侾丏俀亊侾侽侾侽乛俫 |  |
| 丂椡丂丂乲俶乴丂丗丂 | 侽 | 侾.侾亊侾侽俋乛俫 | 侾丏俀亊侾侽侾侽乛俫 |
| 丂俫亙俼侾丂 | 丂俼侾亙俫亙俼俀丂 | 丂俼俀亙俫丂 | 揹婥椡慄 | |
| 揹丂奅乲俶乛俠乴丗丂 | 侽 | 侾.俉亊侾侽侾侽乛俫 | 侽 |  |
| 丂椡丂丂乲俶乴丂丗丂 | 侽 | 侾.俉亊侾侽侾侽乛俫 | 侽 |
III丂敿宎俼乲倣乴偺墌拰忬偵扨埵懱愊摉偨傝兿乲俠乛倣俁乴偱揹壸偑暘晍偟偰偄傞丅
嘆丂墌拰偺拞怱偐傜奜曽岦偵俫乲倣乴偺埵抲偱偺揹奅傪媮傔傛丅
夝愢偺儁乕僕傪嶲峫偵偟偰丄僈僂僗偺掕棟傪巊偆丅揹奅偼丄拰偺拞怱幉偵懳偟偰悅捈側曽岦偵側傞丅
| 俫亙俼偺偲偒丂丗 | 丂丂俤亖 | 兾俫俀兿 俀兾兠侽俫 | 亖 | 俫兿 俀兠侽 | 乲倁乛倣乴 |
| 俼亙俫偺偲偒丂丗 | 丂丂俤亖 | 兾俼俀兿 俀兾兠侽俫 | 亖 | 俼俀兿 俀兠侽俫 | 乲倁乛倣乴 |
俥亖俻俤偱偁傞偐傜丄揹奅偲摨偠曽岦偵椡偼摥偔丅乮俻亙侽偺偲偒偼丄揹奅偲偼媡曽岦偵椡傪庴偗傞丅乯
| 俫亙俼偺偲偒丂丗 | 丂丂俥亖 | 兾俫俀兿俻 俀兾兠侽俫 | 亖 | 俫兿俻 俀兠侽 | 乲俶乴 |
| 俼亙俫偺偲偒丂丗 | 丂丂俥亖 | 兾俼俀兿俻 俀兾兠侽俫 | 亖 | 俼俀兿俻 俀兠侽俫 | 乲俶乴 |
| 丂俫亙俼丂 | 丂俼亙俫丂 | 揹婥椡慄 | |
| 揹丂奅乲俶乛俠乴丗丂 | 俆.俇亊侾侽侾侽俫 | 侾.係亊侾侽侾侽乛俫 |  |
| 丂椡丂丂乲俶乴丂丗丂 | 俆.俇亊侾侽侾侽俫 | 侾.係亊侾侽侾侽乛俫 |
IV丂岤偝偺柍帇偱偒傞暯斅忬偵扨埵柺愊摉偨傝冃乲C乛倣俀乴偱揹壸偑暘晍偟偰偄傞丅
嘆丂暯斅偐傜悅捈曽岦偵俫乲倣乴偺埵抲偱偺揹奅傪媮傔傛丅
夝愢偺儁乕僕傪嶲峫偵偟偰丄僈僂僗偺掕棟傪巊偆丅揹奅偼丄柺偵悅捈側曽岦偵側傞丅柺偐傜墦偞偐傞曽岦偵惓偺曽岦傪偲傞丅
| 丂丂俤亖 | 冃 俀兠侽 | 乲倁乛倣乴 |
俥亖俻俤偱偁傞偐傜丄揹奅偲摨偠曽岦偵椡偼摥偔丅乮俻亙侽偺偲偒偼丄揹奅偲偼媡曽岦偵椡傪庴偗傞丅乯
| 丂丂俥亖 | 冃俻 俀兠侽 | 乲俶乴 |
V丂岤偝倲乲倣乴偺暯斅忬偵扨埵懱愊摉偨傝兿乲俠乛倣俁乴偱揹壸偑暘晍偟偰偄傞丅暯斅偺拞怱偐傜奜曽岦偵俫乲倣乴偺埵抲偱偺揹奅傪媮傔傛丅
夝愢偺儁乕僕傪嶲峫偵偟偰丄僈僂僗偺掕棟傪巊偆丅揹奅偼丄柺偵悅捈側曽岦偵側傞丅柺偐傜墦偞偐傞曽岦偵惓偺曽岦傪偲傞丅
暯柺偵懳偟偰悅捈側拰傪峫偊傞丅偙偺拰偵偮偄偰暯柺偺拞怱傪拞怱偲偟偰忋壓偵倶偺挿偝偱悅捈偵愗傝庢偭偨拰忬偺暵嬋柺傪峫偊傞丅忋壓柺偱揹奅偲柺偼悅捈 懁柺偱揹奅偼柺偲暯峴側偺偱丄揹奅傪愊暘偡傞偲忋壓柺偩偗偑侽偱側偄抣傪庢傞丅傑偨丄暵嬋柺偼揹壸暘晍偵懳偟偰懳徧側偺偱丄 忋柺壓柺偱揹奅偼乮悅捈奜岦偒偱乯摨偠偱丄柺忋偱揹奅偺戝偒偝偼摍偟偄丅 忋乮壓乯柺偺柺愊傪俽偲偡傟偽丄暵嬋柺撪偺揹壸検偼丄|H|亙t乛俀偺偲偒俀|H|俽兿丄|H|亜t乛俀偺偲偒t俽兿偲側傞丅 揹奅偺柺愊暘偼俀俽俤偱偁傞丅備偊偵戝偒偝俤偼
|H|亙t乛俀偺偲偒丂俀俽俤亖俀|H|俽兿/兠0丂仺丂俤亖兿|H|/兠0
|H|亜t乛俀偺偲偒丂俀俽俤亖兿t俽/兠0丂仺丂俤亖兿t/俀兠0
揹奅偼丄拞怱偐傜奜偵岦偐偆曽岦丅拞怱偐傜嫍棧偵斾椺偟偰揹奅偼戝偒偔側傞丅乮揹婥椡慄偑岤偝偵斾椺偟偰憹壛偟偰偄偔丅乯柺偺奜偱揹奅偼堦掕偵側傞丅
VI丂揰乮侽.侾丆侽乯乲倣乴偵侾乲俠乴偺揹壸丄揰乮亅侽.侾丆侽乯乲倣乴偵亅侾乲俠乴偺揹壸偑偁傞丅
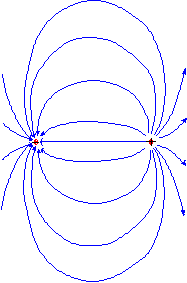
嘆丂乮侽丆侾乯乲倣乴偱偺揹奅傪媮傔傛丅
丂丂俤亖乮亅侾丏俉亊侾侽俋丆侽乯乲俶乛俠乴
嘇丂乮侽丆亅侾乯乲倣乴偱偺揹奅傪媮傔傛丅
丂丂俤亖乮亅侾丏俉亊侾侽俋丆侽乯乲俶乛俠乴
嘊丂乮侾丆侽乯乲倣乴偱偺揹奅傪媮傔傛丅
丂丂俤亖乮俁丏俇亊侾侽俋丆侽乯乲俶乛俠乴
嘋丂揹婥椡慄傪昤偗丅