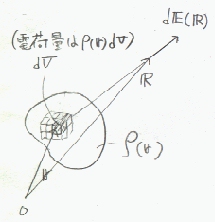
 空間を'点と見なせるほどに'微小な立体で(埋め尽すように)区切って、それぞれの微小な立体の中に含まれる電荷量をその場所の'点'電荷量とみなして、着目する点Rに及ぼす電界
空間を'点と見なせるほどに'微小な立体で(埋め尽すように)区切って、それぞれの微小な立体の中に含まれる電荷量をその場所の'点'電荷量とみなして、着目する点Rに及ぼす電界
 空間を'点と見なせるほどに'微小な立体で(埋め尽すように)区切って、それぞれの微小な立体の中に含まれる電荷量をその場所の'点'電荷量とみなして、着目する点Rに及ぼす電界
空間を'点と見なせるほどに'微小な立体で(埋め尽すように)区切って、それぞれの微小な立体の中に含まれる電荷量をその場所の'点'電荷量とみなして、着目する点Rに及ぼす電界
| ⊿E(R)= | ρ(r)⊿V | R-r | ・・・(1) | |
| 4πε0|R-r|2 | |R-r| |
となる。この電界を電荷の分布する総ての空間について(⊿V(r)に関して)たせば、
| E(R)=Σ⊿E(R)=Σ | ρ(r)⊿V | R-r | |
| 4πε0|R-r|2 | |R-r| |
| =∫ | ρ(r)d V | R-r | ・・・(2) | |
| 4πε0|R-r|2 | |R-r| |
一般に、空間にどのように電荷が分布してもかまわない。但し、積分はrに関して全空間にわたって行なう。(体積積分を行なう)
(積分する為に空間に対して容易に座標(変数)が設定できるのは、厚みのある平面(はんぺん)、球、円柱のような対称な電荷分布に対してである。)
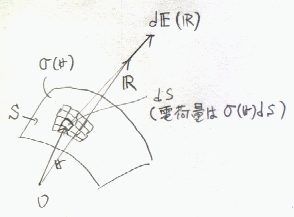 電荷の分布する面Sを微小な面で(埋め尽すように)区切れば、平面では厚さは無視できるほど薄いので、それぞれの区切られた微小な面は3次元の空間で点とみなすことができる。それぞれの微小な面の中に含まれる電荷量をその点の’点電荷量’として、着目する点Rでの電界
電荷の分布する面Sを微小な面で(埋め尽すように)区切れば、平面では厚さは無視できるほど薄いので、それぞれの区切られた微小な面は3次元の空間で点とみなすことができる。それぞれの微小な面の中に含まれる電荷量をその点の’点電荷量’として、着目する点Rでの電界
点r(もちろん電荷の分布する面S上にある)における電荷
| ⊿E(R)= | σ(r)⊿S | R-r | ・・・(3) | |
| 4πε0|R-r|2 | |R-r| |
となる。この電界を総ての⊿Sなる大きさの'点電荷'について(rに関して)たせば、
| E(R)=Σ⊿E(R)=Σ | σ(r)⊿S | R-r | |
| 4πε0|R-r|2 | |R-r| |
| =∫ | σ(r)d S | R-r | ・・・(4) | |
| 4πε0|R-r|2 | |R-r| |
但し、積分はrに関して面全体にわたって行なう。(面積分を行なう)
一般には、Sはどのような面でもかまわない。(球殻でも、円筒でも、もっと複雑な曲面でもよい)
(積分する為に面に対して容易に座標(変数)が設定できるのは、平面、球殻、円筒の電荷分布である。)
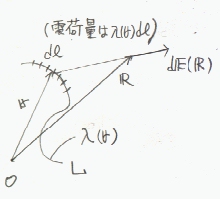 電荷の分布する線Lをごく短い線で区切って、それぞれのごく短い線を点とみなし、それぞれのごく短い線の中に含まれる電荷量をその点電荷量として、着目する点Rでの電界
電荷の分布する線Lをごく短い線で区切って、それぞれのごく短い線を点とみなし、それぞれのごく短い線の中に含まれる電荷量をその点電荷量として、着目する点Rでの電界
ごく短い線の長さを
点r(もちろん電荷の分布する直線L上にある)における電荷
| ⊿E(R)= | λ(r)⊿L | R-r | ・・・(5) | |
| 4πε0|R-r|2 | |R-r| |
となる。この電界をL上の総ての点について(rに関して)たせば、
| E(R)=Σ⊿E(R)=Σ | λ(r)⊿L | R-r | |
| 4πε0|R-r|2 | |R-r| |
| =∫ | λ(r)d L | R-r | ・・・(6) | |
| 4πε0|R-r|2 | |R-r| |
但し、積分はrに関して線全体にわたって行なう。
一般には、Lはどのような線でもかまわない。(直線でも、円環でも、複雑に曲がった線でも良い。)
(積分する為に線に対して容易に座標(変数)が設定できるのは、直線、円環の場合である。もし、電荷が直線状に分布すれば、直線の方向にZ軸をとって、