偙偺儁乕僕偼丄
Friday, 29-Jun-2001 12:43:08 JST偵峏怴偝傟傑偟偨丅
偙偺儁乕僕偼丄乫屻摗 塸梇仐揹婥揹巕僔僗僥儉岺妛壢丂拞晹戝妛乫偑嶌惉偟偰偄傑偡丅
幙栤丄楢棈偼丄屻摗仐揹婥揹巕僔僗僥儉岺妛壢傊偍婅偄偟傑偡丅
'99丂11/25 儗億乕僩偺棯夝乮夝愢乯
嘥丂揰侾乮埵抲儀僋僩儖俼1乯偵俻1乮俠乯丄揰俀乮埵抲儀僋僩儖俼2乯偵俻2乮俠乯丄
揰俁乮埵抲儀僋僩儖俼3乯偵俻3乮俠乯偺揰揹壸偑偁傞丅埲壓偺栤偄偵摎偊傛丅
嘆丂揰侾偺揹壸偺惷揹億僥儞僔儍儖僄僱儖僊乕傪媮傔傛丅
嘇丂揰倰(埵抲儀僋僩儖倰乯偵偍偗傞揹埵傪媮傔傛丅
嘊丂揰俼(埵抲儀僋僩儖俼乯偵偍偗傞揹奅傪媮傔傛丅
嘋丂俼1亖乮侾丆侽丆侽乯乮倣乯丄俼2亖乮侽丆侾丆侽乯乮倣乯丄俼3亖乮侽丆侽丆侾乯乮倣乯丄俻1亖俻2亖俻3亖侾亊侾侽-8乮俠乯偺偲偒丄揰俀偺揹壸偺惷揹億僥儞僔儍儖僄僱儖僊乕傪媮傔傛丅
嘍丂俼1亖乮侾丆侽丆侽乯乮倣乯丄俼2亖乮侽丆侾丆侽乯乮倣乯丄俼3亖乮侽丆侽丆侾乯乮倣乯丄俻1亖俻2亖亅俻3亖侾亊侾侽-8乮俠乯偺偲偒丄揰俀偺揹壸偺惷揹億僥儞僔儍儖僄僱儖僊乕傪媮傔傛丅
嘐丂嘋丆嘍偵偍偄偰丄揰乮侽丆侽丆侽乯乮倣乯丄揰乮侾丆侾丆侾乯乮倣乯丄揰乮侾丆侾丆侽乯乮倣乯偺偦傟偧傟偺揰偵偍偗傞揹埵偲揹奅傪媮傔傛丅
夝摎椺
嘆丂揰侾偺揹埵偵揹壸傪偐偗傟偽摼傜傟傞丅揰侾偺揹埵偼丄揰俀偲揰俁偺偦傟偧傟偺揹壸偵傛傝梌偊傜傟傞揹埵傪懌偣偽傛偄丅
丂冇亖俻2/係兾兠0乥俼1亅俼2乥亄
俻3/係兾兠0乥俼1亅俼3乥 [V]
丂備偊偵丄惷揹億僥儞僔儍儖僄僱儖僊乕倂偼丄
丂倂亖俻1冇亖俻1/係兾兠0乮俻2/乥俼1亅俼2乥亄
俻3/乥俼1亅俼3乥乯 [J]
嘇丂俻1乣俻3偺偦傟偧傟偺揰揹壸偵傛傝梌偊傜傟傞揹埵傪懌偣偽傛偄偺偱丄
丂冇乮倰乯亖俻1/係兾兠0乥倰亅俼1乥亄
俻2/係兾兠0乥倰亅俼2乥亄俻3/係兾兠0乥倰亅俼3乥 [V]
嘊丂慜夞乮'99/10/21乯偲摨條偵丄揰揹壸偺嶌傞揹奅傪懌偣偽摼傜傟傞丅
丂俤亖俻1/乮係兾兠0乥俼亅俼1乥2乯丒
乮俼亅俼1乯乛乥俼亅俼1乥亄
俻2/乮係兾兠0乥俼亅俼2乥2乯丒
乮俼亅俼2乯乛乥俼亅俼2乥亄
俻3/乮係兾兠0乥俼亅俼3乥2乯丒
乮俼亅俼3乯乛乥俼亅俼3乥 [N/C]([V/m])
嘊丂暿夝
揹奅偲揹埵偲偺娭學丄俤亖亅grad冇乮亖亅佫冇乯 偵傛傝丄揹奅傪媮傔傞丅
堦斒偵丄佫乮侾乛乥倰亅俼i乥乯亖亅乮倰亅俼i乯乛乥倰亅俼i乥3 偑惉傝棫偮偙偲傪棙梡偟偰丄
俤乮倰乯亖亅佫冇亖亅佫乮俻1/係兾兠0乥倰亅俼1乥亄
俻2/係兾兠0乥倰亅俼2乥亄俻3/係兾兠0乥倰亅俼3乥乯
丂丂亖俻1/係兾兠0丒乮亅佫乮侾乛乥倰亅俼1乥乯亄
俻2/係兾兠0丒乮亅佫乮侾乛乥倰亅俼2乥乯亄俻3/係兾兠0丒乮亅佫乮侾乛乥倰亅俼3乥乯
丂丂亖俻1/係兾兠0丒乮倰亅俼1乯乛乥倰亅俼1乥3亄
俻2/係兾兠0丒乮倰亅俼2乯乛乥倰亅俼2乥3亄
俻3/係兾兠0丒乮倰亅俼3乯乛乥倰亅俼3乥3 [N/C]([V/m])
倰亖俼偱偁傞偐傜丄
丂俤乮俼乯亖俻1/係兾兠0丒乮俼亅俼1乯乛乥俼亅俼1乥3亄
俻2/係兾兠0丒乮俼亅俼2乯乛乥俼亅俼2乥3亄
俻3/係兾兠0丒乮俼亅俼3乯乛乥俼亅俼3乥3 [N/C]([V/m])
嘋丂嘆偺昞尰傪嶲峫偵偟偰昞尰偡傟偽丄揰俀偺揹壸偺惷揹億僥儞僔儍儖僄僱儖僊乕倂偼丄
丂倂亖俻2/係兾兠0丒乮俻1/乥俼2亅俼1乥亄
俻3/乥俼2亅俼3乥乯
偱偁傞偐傜丄悢抣傪戙擖偡傟偽丄
俼2亅俼1亖乮亅侾丆侾丆侽乯
俼2亅俼3亖乮侽丆侾丆亅侾乯
丂偙偺昞尰偲丂俻1亖俻2亖俻3亖侾亊侾侽-8乮俠乯丂傪峫椂偟偰丄悢抣偵捈偣偽丄
侾/係兾兠0亖俋亊侾侽9偲偟偰丄
丂倂亖俋亊侾侽-7乛俀1/2亄俋亊侾侽-7乛俀1/2
丂丂亖俋丒俀1/2亊侾侽-7丂[J]
偱梌偊傜傟傞丅
嘍丂嘋偲摨條偵偟偰峴偆丅
嘆偺昞尰傪嶲峫偵偟偰昞尰偡傟偽丄揰俀偺揹壸偺惷揹億僥儞僔儍儖僄僱儖僊乕倂偼丄
丂倂亖俻2/係兾兠0丒乮俻1/乥俼2亅俼1乥亄
俻3/乥俼2亅俼3乥乯
偱偁傞偐傜丄悢抣傪戙擖偡傟偽丄
俼2亅俼1亖乮亅侾丆侾丆侽乯
俼2亅俼3亖乮侽丆侾丆亅侾乯
丂偙偺昞尰偲丂俻1亖俻2亖亅俻3亖侾亊侾侽-8乮俠乯丂傪峫椂偟偰丄悢抣偵捈偣偽丄
侾/係兾兠0亖俋亊侾侽9偲偟偰丄
丂倂亖俋亊侾侽-7乛俀1/2亅俋亊侾侽-7乛俀1/2亖侽丂[J]
偱梌偊傜傟傞丅
嘐丂揹埵偼嘇傪丄揹奅偼嘊傪嶲峫偵偡傞丅
亅亅亅嘋偺忦審偵懳偟偰
揹奅媦傃揹埵傪抦傝偨偄嵗昗傪乮倶丆倷丆倸乯偲昞偣偽丄乮侾乛係兾兠0亖俋亊侾侽9偲偟偰丄乯
侾偺揹壸偵傛傞揹埵冇1媦傃丄揹奅俤1偼丄
丂冇1亖俋亊侾侽9亊侾亊侾侽-8乛乮乮倶亅侾乯2亄倷2亄倸2乯1/2
丂丂丂丂亖俋侽乛乮乮倶亅侾乯2亄倷2亄倸2乯1/2 [V]
丂俤1亖俋亊侾侽9亊侾亊侾侽-8乛乮乮倶亅侾乯2亄倷2亄倸2乯3/2
丒乮倶亅侾丆倷丆倸乯
丂丂亖俋侽乛乮乮倶亅侾乯2亄倷2亄倸2乯3/2丒乮倶亅侾丆倷丆倸乯 [v/m]
摨條偵丄俀偺揹壸偵傛傞揹埵冇2媦傃丄揹奅俤2偼丄
丂冇2亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄乮倷亅侾乯2亄倸2乯1/2
丂丂丂丂亖俋侽乛乮倶2亄乮倷亅侾乯2亄倸2乯1/2 [V]
丂俤2亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄乮倷亅侾乯2亄倸2乯3/2
丒乮倶丆倷亅侾丆倸乯
丂丂亖俋侽乛乮倶2亄乮倷亅侾乯2亄倸2乯3/2丒乮倶丆倷亅侾丆倸乯 [v/m]
摨條偵丄俁偺揹壸偵傛傞揹埵冇3媦傃丄揹奅俤3偼丄
丂冇3亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄倷2亄乮倸亅侾乯2乯1/2
丂丂丂丂亖俋侽乛乮倶2亄倷2亄乮倸亅侾乯2乯1/2 [V]
丂俤3亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄倷2亄乮倸亅侾乯2乯3/2
丒乮倶丆倷丆倸亅侾乯
丂丂亖俋侽乛乮倶2亄倷2亄乮倸亅侾乯2乯3/2丒乮倶丆倷丆倸亅侾乯 [v/m]
丂偦傟偧傟偵丄嵗昗傪戙擖偟偰壛偊傟偽傛偄丅
乮侽丆侽丆侽乯偱偼丄
丂丂冇亖俀俈侽[V]
丂丂俤亖俋侽乮亅侾丆亅侾丆亅侾乯亖乮亅俋侽丆亅俋侽丆亅俋侽乯亖俋侽丒俁1/2乮亅俁-1/2丆亅俁-1/2丆亅俁-1/2乯[V/m]
乮侾丆侾丆侾乯偱偼丄
丂丂冇亖俀俈侽丒俀-1/2[V]
丂丂俤亖俋侽丒俀-3/2乮俀丆俀丆俀乯亖乮俋侽丒俀-1/2丆俋侽丒俀-1/2丆俋侽丒俀-1/2乯
亖俋侽丒乮俁乛俀乯1/2乮俁-1/2丆俁-1/2丆俁-1/2乯[V/m]
乮侾丆侾丆侽乯偱偼丄
丂丂冇亖侾俉侽亄俁侽丒俁1/2[V]
丂丂俤亖乮俋侽亄俋侽乛俁3/2丆俋侽亄俋侽乛俁3/2丆亅俋侽乛俁3/2乯
亖乮俋侽亄侾侽丒俁1/2丆俋侽亄侾侽丒俁1/2丆亅侾侽丒俁1/2乯[V/m]
亅亅亅嘍偺忦審偵懳偟偰
揹奅媦傃揹埵傪抦傝偨偄嵗昗傪乮倶丆倷丆倸乯偲昞偣偽丄乮侾乛係兾兠0亖俋亊侾侽9偲偟偰丄乯
侾偺揹壸偵傛傞揹埵冇1媦傃丄揹奅俤1偼丄
丂冇1亖俋亊侾侽9亊侾亊侾侽-8乛乮乮倶亅侾乯2亄倷2亄倸2乯1/2
丂丂丂丂亖俋侽乛乮乮倶亅侾乯2亄倷2亄倸2乯1/2 [V]
丂俤1亖俋亊侾侽9亊侾亊侾侽-8乛乮乮倶亅侾乯2亄倷2亄倸2乯3/2
丒乮倶亅侾丆倷丆倸乯
丂丂亖俋侽乛乮乮倶亅侾乯2亄倷2亄倸2乯3/2丒乮倶亅侾丆倷丆倸乯 [v/m]
摨條偵丄俀偺揹壸偵傛傞揹埵冇2媦傃丄揹奅俤2偼丄
丂冇2亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄乮倷亅侾乯2亄倸2乯1/2
丂丂丂丂亖俋侽乛乮倶2亄乮倷亅侾乯2亄倸2乯1/2 [V]
丂俤2亖俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄乮倷亅侾乯2亄倸2乯3/2
丒乮倶丆倷亅侾丆倸乯
丂丂亖俋侽乛乮倶2亄乮倷亅侾乯2亄倸2乯3/2丒乮倶丆倷亅侾丆倸乯 [v/m]
摨條偵丄俁偺揹壸偵傛傞揹埵冇3媦傃丄揹奅俤3偼丄
丂冇3亖亅俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄倷2亄乮倸亅侾乯2乯1/2
丂丂丂丂亖亅俋侽乛乮倶2亄倷2亄乮倸亅侾乯2乯1/2 [V]
丂俤3亖亅俋亊侾侽9亊侾亊侾侽-8乛乮倶2亄倷2亄乮倸亅侾乯2乯3/2
丒乮倶丆倷丆倸亅侾乯
丂丂亖俋侽乛乮倶2亄倷2亄乮倸亅侾乯2乯3/2丒乮亅倶丆亅倷丆亅倸亄侾乯 [v/m]
丂偦傟偧傟偵丄嵗昗傪戙擖偟偰壛偊傟偽傛偄丅
乮侽丆侽丆侽乯偱偼丄
丂丂冇亖俋侽[V]
丂丂俤亖俋侽乮亅侾丆亅侾丆侾乯亖乮亅俋侽丆亅俋侽丆俋侽乯亖俋侽丒俁1/2乮亅俁-1/2丆亅俁-1/2丆俁-1/2乯[V/m]
乮侾丆侾丆侾乯偱偼丄
丂丂冇亖俋侽丒俀-1/2亖係俆丒俀1/2[V]
丂丂俤亖俋侽丒俀-3/2乮侽丆侽丆俀乯亖乮侽丆侽丆俋侽丒俀-1/2乯
亖係俆丒俀1/2乮侽丆侽丆侾乯[V/m]
乮侾丆侾丆侽乯偱偼丄
丂丂冇亖侾俉侽亅俁侽丒俁1/2[V]
丂丂俤亖乮俋侽亅俋侽乛俁3/2丆俋侽亅俋侽乛俁3/2丆俋侽乛俁3/2乯
亖乮俋侽亅侾侽丒俁1/2丆俋侽亅侾侽丒俁1/2丆侾侽丒俁1/2乯[V/m]
嘦丂敿宎倎乮倣乯偺柍尷偵挿偄捈慄墌拰忬偵嬒堦偵枾搙兿乮俠乛倣3乯偱揹壸偑暘晍偟偰偄傞丅埲壓偺栤偄偵摎偊傛丅
嘆丂擟堄偺揰偵偍偄偰丄揹奅偼偳偪傜傪岦偄偰偄傞偐丅
嘇丂嵗昗傪揔摉偵愝掕偟偰丄擟堄偺揰偵偍偗傞揹奅傪媮傔傛丅
嘊丂嵗昗傪揔摉偵愝掕偟偰丄擟堄偺揰偵偍偗傞揹埵傪媮傔傛丅墌拰偺拞怱傪揹埵偺婎弨偲偣傛丅
夝摎椺
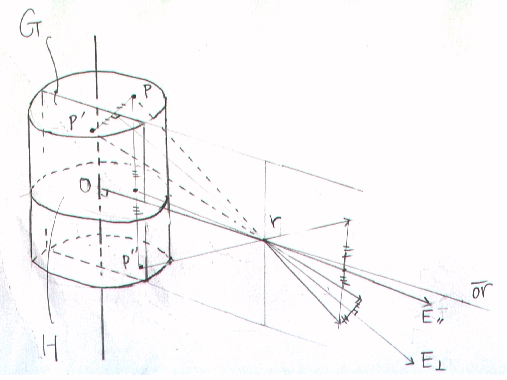
嘆丂揹奅傪抦傝偨偄揰傪倰偲偟丄揰倰傛傝丄墌拰偺拞怱幉偵壓傠偟偨悅慄偺懌傪俷偲偡傞丅
俷傪捠傝丄墌拰偺拞怱幉偵悅捈側柺俧偱丄墌拰傪擇偮偵暘偗傞丅
丂揰揹壸偲尒側偣傞傎偳旝彫側椞堟偵墌拰傪暘偗偰丄偦偺撪偺堦偮偺旝彫椞堟倫偑揰倰偵媦傏偡揹奅傪峫偊傞丅
椞堟倫偺柺俧偵懳偡傞懳徧側椞堟倫乫偵傕摨検偺揹壸偑懚嵼偟丄偦偺揹壸偑揰倰偵媦傏偡揹奅偼丄倫偺嶌傞揹奅偲戝偒偝偑摍偟偔柺俧偵懳偟偰懳徧偱偁傞丅
傛偭偰丄偙偺擇偮偺揹奅傪崌惉偡傞偲柺俧偵悅捈側惉暘偼偆偪徚偟偰丄柺俧撪偺惉暘偩偗偵側傞丅墌拰忋偺慡揹壸偵懳偟偰丄偙偺傛偆側揹壸偺慻偑梌偊傜傟傞偺偱丄
揹奅偼丄柺俧撪偺惉暘偺傒偱梌偊傜傟傞丅
丂偮偓偵丄墌拰偺拞怱幉偲揰倰傪娷傓柺俫傪峫偊丄墌拰偵暘晍偡傞揹壸傪柺俫偱擇偮偺椞堟偵暘偗傞丅
揰揹壸偲尒側偣傞傎偳旝彫側椞堟偵墌拰傪暘偗偰丄偦偺撪偺堦偮偺旝彫椞堟倫偑揰倰偵媦傏偡揹奅傪峫偊傞丅
椞堟倫偺柺俫偵懳偡傞懳徧側椞堟倫"偵傕摨検偺揹壸偑懚嵼偟丄偦偺揹壸偑揰倰偵媦傏偡揹奅偼丄倫偺嶌傞揹奅偲戝偒偝偑摍偟偔柺俫偵懳偟偰懳徧偱偁傞丅
傛偭偰丄偙偺擇偮偺揹奅傪崌惉偡傞偲柺俫偵悅捈側惉暘偼偆偪徚偟偰丄柺俫撪偺惉暘偩偗偵側傞丅墌拰忋偺慡揹壸偵懳偟偰丄偙偺傛偆側揹壸偺慻偑梌偊傜傟傞偺偱丄
揹奅偼丄柺俫撪偺惉暘偺傒偱梌偊傜傟傞丅
備偊偵丄揰倰偵偍偄偰丄柺俧偲柺俫偵娷傑傟傞曽岦乮墌拰偺拞怱幉偵懳偟偰丄悅捈側曽岦乯偵揹奅偼岦偔丅
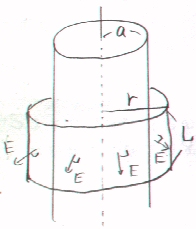
嘇丂墌拰偺拞怱幉偐傜揹奅傪抦傝偨偄揰傑偱偺嫍棧傪倰偲偡傞丅
敿宎倰丄崅偝俴偺墌拰忬偺暵嬋柺傪峫偊偰丄僈僂僗偺掕棟傪揔梡偡傞丅
暵嬋柺忋偱偺揹奅傪俤偲偡傟偽丄
僈僂僗偺掕棟偺嵍曈亖佺俤丒d俽(S:墌拰懁柺+墌拰忋柺亄墌拰壓柺)=佺俤丒d俽(S:墌拰懁柺)+佺俤丒d俽(S:墌拰忋柺+墌拰壓柺)
佺俤丒d俽(S:墌拰懁柺)=俤佺d俽(S:墌拰懁柺)(俤偲d俽偼摨偠曽岦偱丄俤偼柺忋偱摨偠抣)=俤2兾倰俴乮懁柺忋偺揹奅傪俤偲偍偄偨丅乯
佺俤丒d俽(S:墌拰忋柺+墌拰壓柺)=0(柺忋偱俤偲d俽偼悅捈側偺偱撪愊偼0)
僈僂僗偺掕棟偺嵍曈亖俤2兾倰俴
僈僂僗偺掕棟偺塃曈亖佺兿倓倁/兠0
丂丂亖兿/兠0丒兾倰2俴乮丂倰亙倎乯丄兿/兠0丒兾倎2俴丂乮倎亙倰乯
丂俤亖兿倰/俀兠0 [V/m] 丂乮倰亙倎乯
丂俤亖兿倎2/俀兠0倰 [V/m]丂乮倎亙倰乯
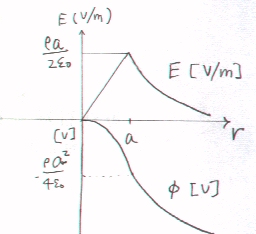
嘊丂揹埵傪抦傝偨偄揰偲墌拰偲偺拞怱幉偲偺嫍棧傪俼偲偡傞丅揹埵傪抦傝偨偄揰偲偙偺揰偐傜墌拰偺拞怱幉偵壓傠偟偨揰傪寢傇慄忋偱丄揹奅傪愊暘偡傞丅
揹奅偺曽岦偲愊暘偺曽岦偼暲峴偱偁傞偐傜丄揹埵冇偼丄
丂冇亖佺亅俤丒倓倰乮倰丟侽乣俼乯亖佺亅俤倓倰乮倰丟侽乣俼乯
丂冇亖佺亅乮兿倰/俀兠0乯倓倰乮倰丟侽乣俼乯丂乮俼亙倎乯亖亅兿俼2/係兠0 [V] 丂乮俼亙倎乯
丂冇亖佺亅乮兿倰/俀兠0乯倓倰乮倰丟侽乣倎乯亅佺兿倎2/俀兠0倰丒倓倰乮倰丟倎乣俼乯乮丂倎亙俼乯
丂丂亖亅兿倎2/係兠0亅 兿倎2/俀兠0倢倧倗乮俼乛倎乯丂乮倎亙俼乯
丂塃偼丄兿亜侽偺帪偺丄揹奅乮墌拰偺拞怱幉偐傜奜偵岦偐偭偰惓乯偲揹埵傪昞偡丅
嘨丂岤偝偺柍帇偱偒傞柍尷偵峀偄斅侾丆俀偑娫妘倓乮倣乯偱暯峴偵偁傞丅偨偩偟丄斅侾偵偼嬒堦偵柺枾搙冃1乮俠乛倣2乯偺揹壸偑丄
斅俀偵偼嬒堦偵柺枾搙冃2乮俠乛倣2乯偺揹壸偑偁傞丅傑偨丄斅俀偐傜斅侾偵岦偐偭偰悅捈偵倸幉傪愝掕偟丄倸幉偺尨揰偼斅俀偵偁傞偲偡傞丅傎偐偵昁梫側嵗昗偍傛傃嵗昗幉偼揔摉偵愝掕偟偰丄埲壓偺栤偄偵摎偊傛丅
嘆丂斅侾偵暘晍偡傞揹壸偵傛傞擟堄偺揰偵偍偗傞揹奅偺戝偒偝偲曽岦傪媮傔傛丅
嘇丂斅俀偵暘晍偡傞揹壸偵傛傞擟堄偺揰偵偍偗傞揹奅傪媮傔傛丅
嘊丂斅侾丆斅俀偺椉曽偵暘晍偡傞揹壸偵傛傞擟堄偺揰偵偍偗傞揹奅傪媮傔傛丅
嘋丂斅俀偺揹埵傪婎弨偲偟偰丄擟堄偺揰偵偍偗傞揹埵傪媮傔傛丅
嘍丂嘊丆嘋偵偍偄偰丄倓亖侾(mm)丄冃1亖冃2亖侾亊侾侽-8乮俠乛倣2乯偺偲偒丄倸嵗昗偺娭悢偲偟偰揹奅偺倸幉惉暘偲揹埵傪僌儔僼壔偣傛丅
嘐丂嘊丆嘋偵偍偄偰丄倓亖侾(mm)丄冃1亖亅冃2亖侾亊侾侽-8乮俠乛倣2乯偺偲偒丄倸嵗昗偺娭悢偲偟偰揹奅偺倸幉惉暘偲揹埵傪僌儔僼壔偣傛丅
夝摎椺
嘆丆嘇丆嘊丂'99 10/21 採弌婜尷偺儗億乕僩嘨傪嶲峫偵偡傞丅丂
嘋 揹奅偼倸幉惉暘偟偐側偄偺偱丄嘊偲摨條偵偟偰摼傜傟傞乮壓偵昞偝傟傞乯揹奅俤乮倅乯傪倸偵偮偄偰愊暘偡傟偽揹埵偑摼傜傟傞丅
丂俤乮倅乯亖冃1乛俀兠0丒乮倅亅倓乯乛|倅亅倓|亄冃2乛俀兠0丒倅乛|倅|丂[N/C]([V/m])
丂応崌暘偗偟偰昞偣偽丄
丂俤1乮倅乯亖乮冃1亄冃2乯乛俀兠0丂乮倅亜倓乯
丂俤2乮倅乯亖乮亅冃1亄冃2乯乛俀兠0丂乮倓亜倅亜侽乯
丂俤3乮倅乯亖亅乮冃1亄冃2乯乛俀兠0丂乮侽亜倅乯
揹埵傪抦傝偨偄揰傪倸亖俫偲偡傟偽丄揹埵冇乮俫乯偼丄
丂冇乮俫乯亖佺亅俤乮倸乯倓倸乮倸丟侽乣俫乯亖佺亅俤3乮倸乯倓倸乮倸丟侽乣俫乯丂乮俫亙侽乯
丂丂丂亖佺亅俤2乮倸乯倓倸乮倸丟侽乣俫乯丂乮侽亙俫亙倓乯
丂丂丂亖佺亅俤1乮倸乯倓倸乮倸丟倓乣俫乯亄冇乮倓乯丂乮倓亙俫乯
丂俫亙侽丂偺偲偒
丂冇亖佺亅俤3乮倸乯倓倸乮倸丟侽乣俫乯亖乮冃1亄冃2乯俫乛俀兠0丂[V]
丂侽亙俫亙倓丂偺偲偒
丂冇亖佺亅俤2乮倸乯倓倸乮倸丟侽乣俫乯乮侽亙俫亙倓乯亖乮冃1亅冃2乯俫乛俀兠0丂[V]
丂冇乮倓乯亖乮冃1亅冃2乯倓乛俀兠0丂[V]
丂倓亙俫丂偺偲偒
丂冇亖佺亅俤1乮倸乯倓倸乮倸丟倓乣俫乯亄冇乮倓乯亖亅乮冃1亄冃2乯乮俫亅倓乯乛俀兠0亄乮冃1亅冃2乯倓乛俀兠0丂[V]
丂丂亖亅乮冃1亄冃2乯俫乛俀兠0亄冃1倓乛兠0丂[V]
嘍丂嘋偵梌偊傜傟偨揹奅偲揹埵偵抣傪戙擖偡傞丅
丂倸亙侽丂偺偲偒
丂俤乮倸乯亖亅乮冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖乮冃1亄冃2乯倸乛俀兠0丂[V]
丂侽亙倸亙倓丂偺偲偒
丂俤乮倸乯亖乮亅冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖乮冃1亅冃2乯倸乛俀兠0丂[V]
丂倓亙倸丂偺偲偒
丂俤乮倸乯亖乮冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖亅乮冃1亄冃2乯倸乛俀兠0亄冃1倓乛兠0丂[V]
偱偁傞偐傜丄埵抲傪倸(m)偲偡傟偽丄侾乛兠0亖侾乛俉丏俉俆係亊侾侽-12亖侾丏侾俁亊侾侽11偱偁傞偙偲傪峫椂偟偰丄
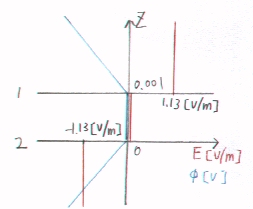
丂倸亙侽丂偺偲偒
丂俤乮倸乯亖亅侾丏侾俁丂[N/C]乮[V/m]乯
丂冇乮倸乯亖侾丏侾俁倸[V]
丂侽亙倸亙倓丂偺偲偒
丂俤乮倸乯亖侽丂[N/C]乮[V/m]乯
丂冇乮倸乯亖侽丂[V]
丂倓亙倸丂偺偲偒
丂俤乮倸乯亖侾丏侾俁丂[N/C]乮[V/m]乯
丂冇乮倸乯亖亅侾丏侾俁乮倸亅侽丏侽侽侾乯丂[V]
嘐丂嘋偵梌偊傜傟偨揹奅偲揹埵偵抣傪戙擖偡傞丅
丂倸亙侽丂偺偲偒
丂俤乮倸乯亖亅乮冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖乮冃1亄冃2乯倸乛俀兠0丂[V]
丂侽亙倸亙倓丂偺偲偒
丂俤乮倸乯亖乮亅冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖乮冃1亅冃2乯倸乛俀兠0丂[V]
丂倓亙倸丂偺偲偒
丂俤乮倸乯亖乮冃1亄冃2乯乛俀兠0丂[N/C]乮[V/m]乯
丂冇乮倸乯亖亅乮冃1亄冃2乯倸乛俀兠0亄冃1倓乛兠0丂[V]
偱偁傞偐傜丄埵抲傪倸(m)偲偡傟偽丄侾乛兠0亖侾乛俉丏俉俆係亊侾侽-12亖侾丏侾俁亊侾侽11偱偁傞偙偲傪峫椂偟偰丄
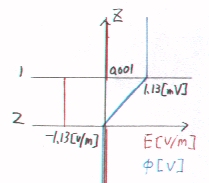
丂倸亙侽丂偺偲偒
丂俤乮倸乯侽丂[N/C]乮[V/m]乯
丂冇乮倸乯亖侽丂[V]
丂侽亙倸亙倓丂偺偲偒
丂俤乮倸乯亖亅侾丏侾俁丂[N/C]乮[V/m]乯
丂冇乮倸乯亖侾丏侾俁倸丂[V]
丂倓亙倸丂偺偲偒
丂俤乮倸乯亖侽丂[N/C]乮[V/m]乯
丂冇乮倸乯亖侾丏侾俁亊侾侽-3丂[V]丂亖侾丏侾俁丂[mV]
嘩丂敿宎倎乮倣乯偺媴忬偵嬒堦偵枾搙兿乮俠乛倣3乯偱揹壸偑暘晍偟偰偄傞丅埲壓偺栤偄偵摎偊傛丅
嘆丂擟堄偺揰偵偍偄偰丄揹奅偼偳偪傜傪岦偄偰偄傞偐丅
嘇丂嵗昗傪揔摉偵愝掕偟偰丄擟堄偺揰偵偍偗傞揹奅傪媮傔傛丅
嘊丂嵗昗傪揔摉偵愝掕偟偰丄擟堄偺揰偵偍偗傞揹埵傪媮傔傛丅
夝摎椺
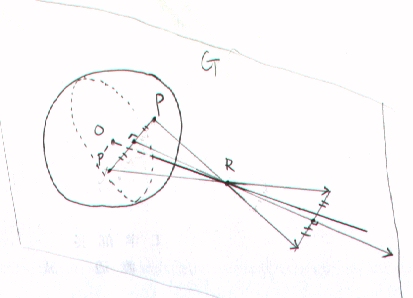
嘆丂揹奅傪抦傝偨偄揰傪俼偲偟丄揰俼偲媴偺拞怱俷傪寢傇慄俷俼傪娷傓暯柺俧傪峫偊傞丅
乮柍悢偺乮曽岦偺乯暯柺偑峫偊傜傟傞偑偦偺偆偪偺堦偮傪慖傇乯
丂揰揹壸偲尒側偣傞傎偳旝彫側椞堟偵媴傪暘偗偰丄偦偺撪偺堦偮偺旝彫椞堟倫偑揰俼偵媦傏偡揹奅傪峫偊傞丅
椞堟倫偺柺俧偵懳偡傞懳徧側椞堟倫乫偵傕摨検偺揹壸偑懚嵼偟丄偦偺揹壸偑揰俼偵媦傏偡揹奅偼丄倫偺嶌傞揹奅偲戝偒偝偑摍偟偔柺俧偵懳偟偰懳徧偱偁傞丅
傛偭偰丄偙偺擇偮偺揹奅傪崌惉偡傞偲柺俧偵悅捈側惉暘偼偆偪徚偟偰丄柺俧撪偺惉暘偩偗偵側傞丅媴撪偺慡揹壸偵懳偟偰丄偙偺傛偆側揹壸偺慻偑梌偊傜傟傞偺偱丄
揹奅偼丄柺俧撪偺惉暘偺傒偱梌偊傜傟傞丅偮偓偵丄慄俷俼傪娷傓俧偲偼堎側傞暯柺俧'傪峫偊傞丅愭傎偳偲摨條偵偟偰揹奅偺曽岦傪峫偊傞偲丄揹奅偼柺俧'撪偺惉暘偺傒偵側傞偙偲偑暘偐傞丅
備偊偵丄揰俼偵偍偄偰丄柺俧偲柺俧'偵娷傑傟傞曽岦乮媴偺拞怱偲俼傪寢傇曽岦乯偵揹奅偼岦偔丅
嘇丂揹奅傪抦傝偨偄揰倰偺媴偺拞怱俷偐傜偺嫍棧傪倰[m]偲偡傞丅
揹奅偼丄媴偺拞怱偲倰傪寢傇曽岦偵偁傞偺偱丄俷傪拞怱偲偡傞媴柺傪峫偊傞偲揹奅偼丄媴柺偲悅捈偵側傞丅乮媴柺偺朄慄偲乮斀乯暲峴乯
偦偙偱丄拞怱傪俷偲偡傞敿宎倰偺媴偺暵嬋柺偱丄僈僂僗偺掕棟傪棙梡偡傞偲丄揹婥帴婥妛I 梫揰偺僐乕僫乕偲摨條偵媮傔傜傟傞丅偁傞偄偼丄揹壸暘晍傪懱愊愊暘乮揹婥帴婥妛I 梫揰偺僐乕僫乕乯偟偰媮傔傞丅
倰亙倎偺偲偒丄丂丂丂丂俤=兿倰/3兠0丂丂丂丂丂丂丂丂丂丂丂丂丂丂[N/C] ( [V/m] )丂乮拞怱偐傜奜偵岦偐偆曽岦乯
倎亙倰偺偲偒丄丂丂丂丂俤=兿倎3/3兠0倰2丂[N/C] ( [V/m] )丂乮拞怱偐傜奜偵岦偐偆曽岦乯
嘊丂揹埵傪抦傝偨偄揰俼偺媴偺拞怱俷偐傜偺嫍棧傪俼[m]偲偡傞丅
揹埵冇偼丄揹奅傪愊暘偡傟偽摼傜傟傞偺偱丄揹埵偺婎弨傪柍尷墦偵偲偭偰丄
丂冇乮俼乯亖佺亅俤倓倰乮倰丟亣乣俼乯
倎亙俼偺偲偒
丂丂冇乮俼乯亖佺亅俤倓倰乮倰丟亣乣俼乯亖佺亅兿倎3/3兠0倰2倓倰乮倰丟亣乣俼乯
丂丂丂丂丂丂亖兿倎3/3兠0俼丂[V]
倰亙倎偺偲偒
丂丂冇乮俼乯亖佺亅俤倓倰乮倰丟倎乣俼乯亖佺亅兿倰/3兠0倓倰乮倰丟倎乣俼乯
丂丂丂丂丂丂亖亅兿俼2/6兠0亄兿倎2/6兠0亄兿倎3/3兠0倎丂[V]
丂丂丂丂丂丂亖亅兿俼2/6兠0亄兿倎2/2兠0丂[V]
媴撪偺慡揹壸検俻乮俠乯乮亖係兾倎3兿乛俁乯偱偐偒側偍偡偲
倎亙俼偺偲偒
丂丂冇乮俼乯亖兿倎3/3兠0俼丂[V]
丂丂丂丂丂丂亖俻乛係兾兠0俼丂[V]丂乮揰揹壸偺応崌偲摨堦偺昞尰偵側傞乯
倰亙倎偺偲偒
丂丂冇乮俼乯亖亅兿俼2/6兠0亄兿倎2/6兠0亄兿倎3/3兠0倎丂[V]
丂丂丂丂丂丂亖乮倎2亅俼2乯俻乛俉兾兠0倎3亄俻乛係兾兠0倎丂[V]
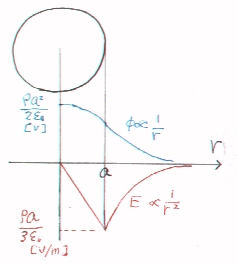
揹奅偲揹埵偼丄塃偺傛偆偵梌偊傜傟傞丅乮兿亙侽偲偍偄偨丅乯
偙傟偱偙偺崁栚偼廔傢傝
揹婥帴婥妛IA儗億乕僩偺堦棗傊栠傞
揹婥帴婥妛IA傊栠傞
揹婥帴婥妛(IA+IB)儗億乕僩偺堦棗傊栠傞
揹婥帴婥妛(IA+IB)傊栠傞






